дачи необходимо умножить на поправочный коэффициент ej,,; определяемый как

ER=l-\-mdJR,, (8.26)

где - диаметр канала; - радиус кривизны канала по оси.

Если вулканизация протекает в условиях конденсации влаги на поверхности вулканизуемого изделия, например при вулканизации в среде насыщенного пара, то теплоотдача возрастает, и коэффициент теплоотдачи можно рассчитать следующим образом:

а=0,72 4

Рп(н.п покр.ср)

(8.27)

t}„=200

вулканизация

Окяажде-ние

где у„ -плотность пара; Х„ - коэффициент теплопроводности пара на линии насыщения; г„-скрытая теплота парообразования; Рп - вязкость пара; &н.п-температура насыщенного пара; Эпокр.ср-средняя температура поверхности вулканизуемого изделия.

В качестве температуры кабельного изделия на выходе может быть принята температура вулканизующей среды с последующим уточнением по результатам определения фактического изменения температуры изделия в процессе движения внутри вулканизационной трубы.

Далее с использованием (8.9) или (8.12) в зависимости от интенсивности теплоотдачи определяется зависимость температуры нагрева внутреннего слоя Эв от времени нагрева t в вулканизационной камере. Такая зависимость для резинового щланга толщиной 5 мм при внутреннем диаметре 40 мм показана на рис. 8.3. Необходимость определения этой зависимости применительно к температуре внутреннего слоя понятна, так как внутренние слои прогреваются значительно медленнее, чеМ наружные. Технологический режим вулканизации до жен быть выбран tiikhM, чтобы внутренние слои по-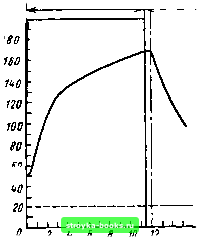

г, мин

Рис. 8.3. Зависимость температуры на наружной и внутренней поверхностях резинового шланга при его вулканизации от времени

лимерного покрытия были вулканизованы полностью, а наружные не были перевулканизованы, так как они большее, время находятся в условиях повышенной температуры и вулканизационной среды. Поэтому степень вулканизации в любой точке покрытия должна быть такова, чтобы физико-механические характеристики вулканизированного материала удовлетворяли предъявляемым техническим требованиям.

Для оценки степени вулканизации различных слоев покрытия необходимо определить эффекты вулканизации для этих слоев и сравнить с допустимыми значениями, вычисляемыми для эталонного

50 48

12 10 8 6 4

г 4 6 8 10 12 Г.мии

Рйс. 8.4. Зависимость l-f{i), построенная по данным рис. 8.3

образца применяемого полимерного материала, что делается, как правило, в лабораторных условиях.

Известно, что степень вулканизации количественно характеризуется эффектом вулканизации:

E=\hdt,

(8.28)

где /в-интенсивность вулканизации.

Если рассматривать эталонный образец, для которого значение интенсивности вулканизации равно 1, то допустимые эффекты вулканизации для эталонного образца будут составлять:

Ешы= jdt=t„,i„; о

Эффекты вулканизации внешних и внутренних слоев можно Рассчитывать графоаналитически, для чего перестраивается зависимость температуры слоя от времени /=/(/) (рис. 8.4).

Площадь, ограниченная кривой I=f{t), на том или ином участке будет численно равна эффекту вулканизации данного слоя. Площадь фигуры ОВВ равна эффекту вулканизации внутренней поверхности, а площадь фигуры OOyAA - эффекту вулканизации внешней поверхности.

Следует учитывать, что покрытие подвергается допол-нительной вулканизации в охлаждающей трубе, так как в течение некоторого времени температура внутренних слоев еще достаточна для протекания процесса вулканизации. Эф-фекты вулканизации внутреннего и внешнего слоев покрытия должны быть не менее Еы и не больше Е„„. Если это условие не соблюдается, необходимо изменить условия вул-. канизации, в частности время нахождения кабеля в вулканизационной трубе, и вновь повторить расчет. Чем ближе эффект вулканизации внутреннего слоя к и эффект

вулканизации наружного слоя к /„„д., тем ближе время вулканизации к оптимальному.

Зная время вулканизации и длину вулканизационной камеры L, можно определить скорость движения v вулканизуемого изделия:

v = Llt,. (8.29)

8.1.3. Способ расчета технологических режимов ЛКНВ с учетом теплоемкости токопроводящей жилы. При этом способе расчета принимается во внимание теплоемкость .vIeтaлличecкoй жилы. Температура по всему сечению жилы практически одинакова, так как ее температуропроводность исключительно велика.

На границе полимерного покрытия и жилы при г=Го, где Го радиус токопроводящей жилы, имеем [49]

59 , л 5Э

(8.30)

где Ру-тепло, которое выделяется в жиле и идет на нагрев жилы и на теплопередачу в окружающую среду; А,- теплопроводность полимерного покрытия.

Приведем (8.1), (8.2) и (8.30) к безразмерным координатам:

(8.31)

Тогда имеем

x=rlR и Fo = at/R.

дх"" X дх д¥о Соответственно на границе г = Го

х=х, x = ro/.R,

а при отсутствии источников тепла в жиле

, д д¥о дх

(8.32)

где М-постоянная. На границе r = R, х=1

-=(9-9o)Bi. (8.33)

Уравнение (8.31) может быть решено аналитически (если теплоемкость полимерного материала практически не зависит от температуры), а также с помощью ЭВМ.

Рассмотрим аналитическое решение задачи. Если начальная температура полимерного покрытия Энач по всему сечению покрытия одинакова, то в соответствии с [49] это решение в общем виде выглядит следующим образом:

где Ц)с-корни характеристического уравнения LF-NH=0 или

при этом вводим обозначения

u=Js/p;

L = MKnJo(>tli)-Ji(5tn);

ЛГ-Л/хцУо(хм)-У1(кц);

F=BiYo(n)-nXi(n);

Я=вио(ц)-ц11(ц);

ж.нач - начальная температура жилы; Jq, Ji, Yq, У]-цилиндрические функции Бесселя соответственно нулевого и первого порядков, первого и второго рода.

Если радиус жилы мал по сравнению с радиусом изделия По по;шмерному покрытию ("/<0,5), то для расчета можно Использовать, формулы, полученные для сплошного цилиндра.

Если теплоотдача достаточно велика (Bi»l), что харак! терно, например, для нагревания изделия в среде насыщенног(Г пара или охлаждения водой, то с учетом наличия токо проводящей жилы уравнение (8.35) примет следующий вид:Г

(8.36

так как

N Yo(l)

F=BiYo(M), а Я=Вио(й),

при этом (8.34) для расчета температуры может быть npeof разовано следующим образом:

S-S.=(So-S„,)

NJo(iiyx)-L\o(iiyx)

-H?-[LYo(n)-iVYo(n)],= dp

Yo(ц>)Jo(M-J()Yo() ,-f„ d

+ (Гж.„,= Г .,) I

(8.37)

Продифференцировав выражения в знаменателях слагаемых формулы (8.37), можно привести ее к следующему виду:

9 - &„ = (Эо - »нач) G (Fo) + ( Г„,, - Г,, нач)(Fo),

(8.38)

где G(Fo) и F{Fo) - некоторые функции от критерия Fo. Графический метод решения уравнения (8.35) и определение корней приведены в [49].

Если радиус жилы по сравнению с радиусом вулканизуемого покрытия достаточно велик (х>0,5), то при большом значении Bi процесс нагревания протекает значительно быстрее. В этом случае, особенно при х, близких к 1, можно с успехом использовать для приближенных расчетов метод сосредоточенных теплоемкостей. С увеличением значений критерия Bi точность этого метода снижается, однако он незаменим для случая, когда теплоемкость вулканизуемого материала заметно зависит от температуры.

Метод такого расчета изложен в [49]. Прежде всего, предполагается, что вся теплоемкость изоляции сосредоточена на окружности, радиус которой равен среднегеометрическому радиусу изоляции гр - у/Яго. Тогда можно составить схему замещения тепловых процессов, показанную на рис. 8.5. Эта схема составляет по аналогии с электрической цепью, в которой электрические сопротивления заменены тепловыми S, источники 270

Рис. 8.5. Схема замещения тепловых процессов при нестационарном режиме нагрева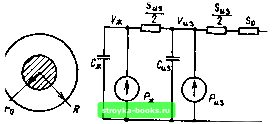

тока-источниками тепловыделения Р и электрические емкости-теплоемкостями элементов конструкции кабельного изделия V.

Затем для каждого элемента конструкции составляется свое дифференциальное уравнение теплового баланса:

(8.39)

где 5„-тепловое сопротивление покрытия; С»-полная теплоемкость жилы (C = cF>);

вж = 9ж~%; вп = 9п -Последует учитывать, что 9„ относится к среднему радиусу покрытия.

Уравнение (8.39) показывает, что теплота, выделяемая в жиле, расходуется на нагрев жилы (в единицу времени) и теплоту, поступающую от жилы к среднему радиусу покрытия.

Аналогично для полимерного покрытия можно записать

(8.40)

где Р„-количество теплоты, выделяющейся в покрытии в единицу времени; С„ -полная теплоемкость покрытия (С =с F)

Jr"" гяап Р™ ™ Р"" совместно уравнения (8.39) и (8.40), получаем

- e*.».,ai-f2

fl -ft

ж.нач «2 + 2.---- I e -

Сж5„

(8.41) 271