
 |
|
Главная Микропроцессорные системы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [ 75 ] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] Типовой алгоритм последовательной обработки дан*» ных в реальном времени, пригодный для вычисления значения e(i) по совокупности N принятых сигналов, подробно рассмотрен в § 5.2. Однако специфика «пачечной» обработки сигналов позволяет существенно упростить этот алгоритм, если длительность сигнальной пачки достаточно мала, чтобы можно было пренебречь изменением полезного параметра за время действия пачки. Например, при радиальной скорости объекта 100 км/ч, ширине диаграммы направленности 10° и скорости вращения антенны 100 об/мин изменение радиальной дальности за время облучения объекта составляет примерно 5 м. Учет такой поправки требуется лишь в специальных прецизионных системах, на которых мы здесь не останавливаемся. Подробный анализ соответствующих упрощенных алгоритмов содержится в [37, 39], где, в частности, проведено сравнение рекуррентного алгоритма оценивания, рассмотренного в § 5.2, с алгоритмом выборочного среднего, который представляется наиболее приемлемым с точки зрения программной обработки массива {8p(i)}. Алгоритм вычисления оценки выборочного среднего в данном случае определяется выражением s{o=Ssy(). где для удобства программной реализации желательно выбрать число N равным степени 2 (т. е. N=2), так как при этом операция деления заменяется циклическим сдвигом. Соответствующая схема алгоритма приведена на рис. 5.26, где использована стандартная процедура т-кратното правого сдвига, рассмотренная в [8] и обозначенная как Shir{z, т). Таким образом, представленный здесь программный блок вычисления вместе с блоком вычисления е, рассмотренным в §5.3, и с операциями (5.15) вычисления 8 и (если они не выполняются аппаратными средствами) составляют программный блок вычисления отклонений принимаемых данных от ожидаемых значений, получаемых в результате обработки этих данных на предшествующих шагах измерительного процесса. 228 7. Контроль достоверности. Вследствие различного рода искажений радиотехнических сигналов принимаемые входные данные могут полностью утрачивать информацию о полезных параметрах (например, при случайных пропаданиях сигнала, связанных с «изрезанно-стью» диаграммы направленности). Такие входные данные можно назвать недостоверными, а соответствующие принятые сигналы - неинформативными. В связи с этим алгоритм обработки данных должен включать в себя операцию проверки информативности принятого сигнала (или достоверности полученных данных) на каждом шаге наблюдения. Смысл этой операции заключается в принятии решения о целесообразности использования входных данных для корректировки измерительного процесса. Если такое решение принимаетя, то дальнейшие вычисления осуществляются в соответствии с выбранным алгоритмом измерения (5.14) (см. также рис. 5.17). Если же принимается противоположное решение, то входные данные отбрасываются, и характер последующих операций определяется специальной управляющей подпрограммой (см. программный блок «Управление измерителем»). Разработка алгоритмов контроля достоверности принимаемых данных в процессе измерения относится к классу задач совместного обнаружения сигналов и оценивания их параметров [48, 49, 63]. Соответствующие оптимальные алгоритмы получаются трудно реализуемыми [50-54], поэтому на практике находят применение лишь самые простые алгоритмы контроля. В данном случае для контроля можно использовать проверку отклонений информационных компонентов от ожидаемых значений. Большие отклонения, превышающие по абсолютной величине некоторый заранее установленный уровень, свидетельствуют о значительных 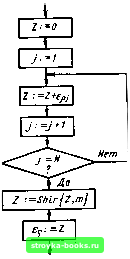 Рис. 5.26. Схема алгоритма вычисления выборочного среднего искажениях принимаемых сигналов, так что соответствующие входные данные могут быть отброшены как недостоверные [52]. Схема программы, реализующей этот алгоритм контроля (рис. 5.27), основана на том, что совокупность импульсных сигналов радиотехнического тракта передает информащ!ю о параметрах и одновременно. Следовательно, наличие импульсов сигнала в стробах дальномерного канала может служить подтверждением достоверности одновременно тех н других наблюдаемых данных- р() и 1(1). Соответствующее решение принимается в результате проверки условия sp(j)<t.p/2, которое означает, что полученное на г-м интервале наблюдения значение тр может быть использовано в измерительном процессе. В противном случае значение (/) отбрасывается как недостоверное, что фиксируется путем присвоения значения 1 операнду Zp, а изъятие e{i) и s{i) из процесса измерений осуществляется с помощью их обнуления. Аналогичные операции выполняются и по отношению к автономным компонентам (г) и e{i). Операнды Zj., Zy, Zy используются в дальнейшем для программного блока „Управление измерителем". Следует заметить, что операция отбрасывания недостоверных данных может выполнятся аппаратно в процессе преобразования аналоговых величин s, и в цифровой код, что уже обсуждалось при рассмотрении особенностей работы преобразователя время-код в качестве измерителя отклонений В результате выполнения рассмотренного программ, ного блока некоторые компоненты вектора (г) -[sp(/) е(/), Sy{i), 8(г)] могут оказаться равными нулю. Такие неинформативные компоненты выпадают из процесса вычислений и ухудшают качество измерительного процесса. Если нарушение информативности входных данных происходит часто, то это свидетельствует о каких-либо нарушениях работоспособности одного из каналов или измерителя в целом. Для обнаружения и локализа- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [ 75 ] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0011 |