г дг 1 дН

(2.6)

Здесь g2 = - kl, g2-поперечная составляющая волнового числа в оболочке световода; Р- коэффициент распространения .в световоде; к2-волновое число оболочки световода с ко-

эффициентом преломления П2, /:2 = /co2 = Cy/iJ,oeo"2 = 2n«2/. ( Для решения данных уравнений исходя из условия, что при г-*оо поле должно стремиться к нулю, следует для г>а использовать цилиндрические функции третьего рода-функции Ганкеля:

. E, = C„Ul,jg2r)e"<e~;

где D„ и С„-постоянные интегрирования; и-порядок функции Ганкеля.

Поперечные составляющие электрических (£,, Е) и магнитных ( г, i/p) полей могут быть выражены с помошрью известных соотношений между поперечными и продольными (£г, Н) составляющими.

Постоянные интегрирования А„, В„, С„, D„ могут быть определены на основании граничных условий. Используем условие равенства тангенциальных составляющих напряжен-ностей электрических и магнитных полей на поверхности раздела сердцевина-оболочка (при г = а):

{а) = Е,2 Н («) = Р2 И; {а)=н2 И; {а)=Н2 (4

Найдя постоянные интегрирования и поставив их в уравнения, после соответствующих преобразований получим следующее трансцендентное уравнение:

" V-al (glfl) У Ца2Н,, [jg2a) 1 ,

gi J,.Ui«) g2iii4jg2a) J «4iJ;.(gifl)./«e«2H;i)(7g2fl)

glci

(2.7)

В результате получаем трансцендентное характеристическое * уравнение, позволяющее определить структуру поля, параметры волн и характеристики волоконного световода. В общем случае уравнение имеет ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны или модой. Но это решение в общем виде весьма сложно,

громоздко. Оно связано с шестью составляющими векторных полей {Е, Е и Н, Я„ Я).

Полученное характеристическое уравнение может быть упрощено для различных частных случаев.

Для симметричных волн, у которых поле не зависит от азимутального угла ф, т. е. т = 0, правая часть характеристического уравнения (2.7) равна нулю и оно распадается на два более простых уравнения:

- Ti-{=--тттггЬ-{ для волн Яо„;

\~ • TTllM \ ДЛЯ волн Com-

(2.8)

Для несимметричных диполъных волн можно получить следующие приближенные уравнения:

J J L!y для .ол„ НЕ.

g.a K{g.a) - g2«Яl)(;g2«) -

(2.9)

Наибольший интерес представляет рассмотрение слабо направляемых волн или волн линейной поляризации LP, которые в основном используются в системах передачи информации по световодам. Это относится к случаю, когда показатель преломления п мало меняется в .поперечном сечении световода, т.е. п1кп2 и Д=(и1-«2)/"i<0,01.

При этом по световоду распространяется практически плоская электромагнитная волна Т с малым углом наклона к оси. Это иллюстрирует рис. 2.13, на котором показано, как с уменьшением угла наклона волны к оси световода 6 уменьшается составляющая Е.

При малых углах наклона волны к оси поперечная составляющая g мала и волновое число к соизмеримо с коэффициентом распространения Р, т.е. /сяР (рис. 2.14). Тогда продольные составляющие поля будут существенно меньше поперечных, т. е. Е<Е и H<Hj. Это позволяет оперировать всего лишь четырьмя составляющими полей вместо шести, которые необходимо учитывать при строгом решении. При этом надлежит решать не сложную векторную задачу, а гораздо более простую-скалярную.

Характеристическое уравнение для LP мод имеет весьма простую форму: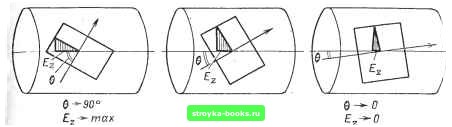

Рис. 2.13. Уменьшение продольной составляюшей с уменьшением наклона

волны в световоде

L+i(gia) A:„+i(g2a)

11 - 1 - к - 1

gl , /, =+g2

(2.10)

Здесь верхние знаки относятся к модам ЕН, а нижние-к модам НЕ.

Для одномодовой системы, которая работает на гибридной волне HEi 1, получаем

4o(g,a) Ko{g2ay

где K{g2a) = H{jg2a)-модифицированная функция Ганкеля.

Сравнивая данные уравнения для линейно поляризованных волн с ранее полученным характеристическим уравнением (2.7) в общем виде, замечаем, что данное уравнение несравненно проще. Оно позволяет элементарно определить структуру поля и характеристики световода для различных типов волн (LP„„).

Из данного уравнения определяем значения g и g2, описывающие поперечное распределение поля; g является :радиальным волновым числом в сердцевине и характеризует

Рис. 2.14. Составляющие волны в общем виде (а) и линейно поляризованной

волны (б)