
 |
|
Главная Развитие оптической связи [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [ 17 ] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] (2.19) где Ак-ширина спектральной линии источника излучения, U равная 1 -3 нм для лазера и 20-40 нм для светоизлучающего « диода; A = («i -M2)/mi; rii и «2-показатели преломления сердцевины и оболочки; /-длина линии; с-скорость света. Для расчета материальной и волноводной дисперсий можно пользоваться также упрощенными формулами и экспериментальными данными: т„,, = ДЯ/М(Я); где М(Я) и В[Х)-удельные материальная и волноводная дисперсии, не/(км • нм). Как видно из рис. 2.28, с увеличением длины волны i материальная дисперсия уменьшается и проходит через нуль, f а волноводная-несколько растет. Причем вблизи Я =1,3 1 происходит их взаимная компенсация и результирующая дис-1 Персия приближается к нулевому значению. Этот эффект I. широко используется в системах передачи по одномодовым I волокнам. Уширение импульса из-за модовой дисперсии, характеризуемое временем нарастания сигнала и определяемое как разность (между самым большим и самым малым временем прихода : в сечение световода на расстоянии / от начала может быть рассчитано по формулам мод = A«i/co-для ступенчатого световода; Смод = АИ1/2со-для градиентного световода, й (Л.), М (Л.), пс/(к м • нм) 160 (2.20) 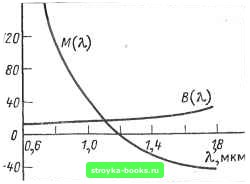 ис. 2.28. Удельные значения дисперсии при различных длинах волн: В(к)- волноводная; М (X) ~ материальная 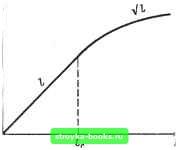 где Д = (и1 -M2)/«i; «i-показатель преломления сердцевины; «2-показатель преломления оболочки; /-длина световода; Со-скорость света. Соответственно пропускная способность градиентного световода в 2/А раз выше, чем у ступенчатого при одинаковом значении А. А так как обычно Ал;1%, пропускные способности указанных световодов могут отличатъ- Рис. 2.29. Длина взаимодействия ся На ДВа ПОряДка. При определении модовой дисперсии следует иметь в виду, что до определенной длины линии /j, нет межмодовой связи, а затем при 1>1с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому, как видно из рис. 2.29, вначале, при 1<1с, дисперсия увеличивается по линейному закону, а затем, при />/t.,-»-no квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии /</с. При длинах линии 1>1 следует пользоваться следующими формулами: i=y/lfc-для ступенчатого световода; Со -для градиентного световода. (2.-21) где /-длина линии; -длина связи мод (ус гановившегося режима). Значение равно 5-7 км Для ступенчатого волокна и 10-15 км-для градиентного. В табл. 2.5 приведены дисперсионные свойства различных типов ВС. Из таблицы видно, что в ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20-50 нс/км). В одномодовых ступенчатых световодах отсутствует модовая дисперсия, и дисперсия в целом сказывается существенно меньше. Здесь проявляются волноводная и материальная дисперсии, и при длине волны порядка 1,3 мкм происходит их взаимная компенсация (ххт) и результирующая дисперсия (Трд=Тмат+вв) минимальна. Однако с учетом затухания предпочтительней длина волны 1,55 мкм, и для достижения минимума дисперсии в этом случае приходится варьировать профилем показателя преломления и диаметром сердцевины волокна. При сложном профиле Таблица 2.S. Дисперсионные свойства различных световодов
можно и на длине волны 1,55 мкм получить минимум дисперсионных искажений. Из рйс. 2.30 видно, что, варьируя диаметром сердцевины, можно сдвинуть дисперсионный ВВ.мат, нс/км ТГрез,нс/км 0,(7J-1 0,03 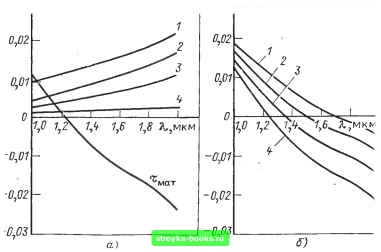 f Рис. 2.30. Зависимость дисперсии от длины волны и диаметра сердцевины одномодовых световодов: о-материальная и волноводная (1-4); У-2п=3,5 мкм; 2-2а=4 мкм; 2а=5 мкм; I 4-2я=10мкм; б-результирующая > [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [ 17 ] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |
||||||||||||||||||||||||||