
 |
|
Главная Развитие оптической связи [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [ 41 ] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] F.,r = KF, (6.6) где -коэффициент жесткости, определяемый опытным путем и зависящий от конструкции кабеля и радиуса ролика. Расчет раздавливающих нагрузок, действующих на ОК при многослойной навивке на барабан, а также натяжения ОК в каком-либо слое навивки приведен в [55]. 6.3. РАСЧЕТ МЕХАНИЧЕСКОЙ ПРОЧНОСТИ ОПТИЧЕСКОГО КАБЕЛЯ И ВЫБОР КОНСТРУКЦИИ Целью расчета механической прочности по заданным нагрузкам является определение возникающих в ОК деформаций, вследствие которых могут возникнуть нежелательные изменения характеристик ОВ. Рассмотрим конструкцию ОК, представленного на рис. 5.2 и 5.3,6. Каждое ОВ в ленте при скрутке ЛЭ закручивается вокруг центральной оси ЛЭ без открутки. Возникающие усилия постоянны и в значительной степени влияют на механическую прочность ОВ, а следовательно, и на долговечность ОВ. Выбор шага скрутки ЛЭ является наиболее важным при производстве данных конструкций ОК. При расчете предположим, что ось ОК представляет собой прямую; ось ЛЭ расположена по спирали с постоянным шагом скрутки на некотором расстоянии от оси ОК; поверхность ЛЭ параллельна оси ОК; площадь поперечного сечения ЛЭ не изменяется при его скручивании; расстояние между ОВ в ЛЭ неизменно; материал покрытия на возникающие в ОВ напряжения не влияет. Если расстояние между осевыми линиями ЛЭ и ОК равно нулю, то это соответствует конструкции, представленной на рис. 5.3, а. При одновременном воздействии на ОК растягивающей, изгибающей и крутящей нагрузок последние две из них на поверхности ОВ имеют максимальное значение. Предположим, что Л-количество ОВ в ЛЭ; d-диаметр ОВ; /);-расстояние между осями ОВ в ЛЭ (/=1,2, Л); Ri-расстояние между осями ОК и ОВ в ЛЭ; v/-угол между осями ОК и ЛЭ; р-шаг скрутки ЛЭ; -расстояние между осями ОК и ЛЭ (рис. 6.1). Линию, соответствующую оси ОВ, можно определить как л:г = Л(С08(б + ф;); y; = i?;Sin(e-b9;); Zi = {pQllii)-Diun, где Q-параметр, определяющий ось ЛЭ; Л, = Ул?-Ь(Асо8)/) (6.8) (6.7) 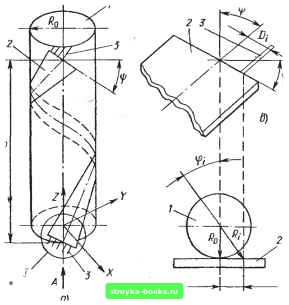 Dj cos Б) Рис. 6.1. Модель для расчета напряжений, возникающих в ОВ при скрутке ЛЭ вокруг центрального силового элемента: а-элемент скрутки; 6-вид по стрелке А; е-область /; /-цштральный силовой элемент; 2-ЛЭ; 5-ОВ tg4),. = Z).-cosil «„; (6.9) (6.10) Нагрузки в ОВ (рис. 6.2) рассчитываются с помощью выражений, приведенных в табл. 6.2, где Е„ -модуль Юнга кварцевого стекла; 1-длина ЛЭ, соответствующая у-му повиву; <jo.B-модуль сдвига (для кварцевого стекла Со.в = 3,2 ГПа); 1/т,--угол скрутки на единицу длины; cs„i-общая нагрузка на ОВ (« + » ставится при растяжении; « -» при сжатии). Рис. 6.2. Распределение напряжений на поверхности ОВ при скрутке ЛЭ Таблица 6.2. Расчет нагрузок в ОВ ОК с ленточными элементами Вид нагрузки Растягивающая (сжимающая) в направлении оси ОВ Изгибающая сг„. Напряжение сдвига Г, Общая а.; ---1 j=yJ(2TiRjY+p (6.11) (6.12) (6.18) Rf+(p/2Ky (6.13) (6.14) Tip la Для Di и Rp при ширине ЛЭ менее 3 мм 2п EdR, а„,„.„,=-3 (6.19) Ti=- (6.15) (6.16) (6.20) + 2Г?] (6.17) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [ 41 ] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |