
 |
|
Главная Развитие оптической связи [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [ 43 ] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86]  Рис. 6.6. Упрощенная модель для расчета деформации ОВ в ТЗО при охлаждении (а), нормальных условиях (б) и нагревании (в) в скрутке: 1-ТЗО; 2-ОВ; 3-сердечник с армирующим элементом Для конструкции ОК с профилированным сердечником (см. рис. 5.1, в) при воздействии растягивающего усилия ОВ перемещается внутри паза. Размер паза определяет допустимую продольную относительную деформацию ОК. Расчет относительного удлинения сердечника ОК с учетом (6.22) осуществлен для модели, представленной на рис. 6.7, в предположении, что ОВ не подвержено воздействию растягивающей силы. При приложении к ОК (сердечнику) растягивающей силы происходит смещение ОВ в пазу до соприкосновения его с дном канавки. Расчетные формулы (6.31, 6.32 и 6.34) приведены в табл. 6.3. Для реверсивной скрутки профилированный сердечник может быть выполнен в виде, представленном на рис. 6.8. В этом случае расчет проводят в соответствии с (6.31, 6.33 и 6.34). Увеличение 8о.к из-за уменьшения р ограничено напряжениями, возникающими в ОВ при малых радиусах изгиба. Разнонаправленная скрутка обеспечивает более точную регулировку натяжения ОВ.   Рис. 6.7. Модель для расчета дефор- Рис. 6.8. Конструкция профилирован- мации ОВ в профилированном сердеч- ного сердечника для разнонаправлен-нике: ной скрутки: i-ОВ; 2-сердечник i-сердечник; 2-паз  Рис.б.Э. Схема расположения ОВ в ОК при его изгибе Представляет интерес определение механической прочности ОК при растяжении исходя из вероятности разрушения ОВ при растяжении. Предположим, что в ОК имеется По в, имеющих одинаковые: длину S., и т - постоянные, определяемые из распределения Вейбулла. Тогда Oo„ = ni-"-Oo, (6.35) где Оор-разрушающее напряжение при вероятности разрыва 63,2%. Изгиб концентрического ОК радиуса R рассмотрим для случая, когда длина осевой линии ОК остается неизменной. Тогда длина деформированной винтовой линии (рис. 6.9) в первом приближении также не меняется. Радиус кривизны р винтовой линии при изгибе меняется от точки к точке. Уравнение винтовой линии можно записать в двух системах координат: в цилиндрической r=R+Acosy(p; z=Asmy(p; (6.36) у = 2кЯ/р в декартовой X = (R+T) cos ц); у = (R+T) sin ц); (6.37) z=Asmyip; T=Acosy(p, где г-радиус; ф - полярный угол; р-шаг винтовой линии; ip=p/R = 2n/y. Участки ОВ, прогнутого с внешней стороны, растягиваются, с внутренней-сжимаются. Вдоль волокна возникают продольные уравновешивающие силы. Рассмотрим два возможных случая расположения ОВ в кабеле: свободное размещение ОВ относительно других элементов конструкции ОК и плотное соединение ОВ с элементами конструкции ОК. При свободной укладке ОВ в ОК, например ОВ в ТЗО или в пазах сердечника, в нем возникают только деформации изгиба, зависящие от его наружного радиуса b и радиуса кривизны р. Наружная часть прогнутого ОВ растягивается, а внутренняя сжимается с ег = Ь р. Напряжения в крайних точках сечения ОВ равны между собой по значению и противоположны по знаку: а+=+8„зг£о- Деформация уменьщается с увеличением шага р. Она также меньше, если радиус скрутки А мал, однако при малых радиусах изгиба R положение меняется: к меньшим деформациям приводит выбор большого А. Продольная уравновешивающая сила может появляться и при свободной укладке ОВ в кабеле вследствие его касания элементов кабеля и проскальзывания при изгибе кабеля. Она зависит от коэффициента трения, характера трения и скорости изгибания. Последняя определяется скоростью намотки ОК на барабан или скоростью прохождения ОК через прогнутый участок при протяжке. С наибольшей скоростью перемещаются точки с 7ф = 71/2 + 71:, т. е. находящиеся посредине между точками Мо и М„. Скорость проскальзывания и соответствующие напряжения увеличиваются с ростом шага скрутки. Для уменьшения напряжений при перемещениях ОВ следует ограничить шаг скрутки, коэффициент трения ОВ и скорость изгибания ОВ. Если ОВ скреплено с демпфером, то его сохранность при изгибе, т. е. его малые деформации, могут быть обеспечены за счет мягкости материала демпфера, который допускает как продольное, так и поперечное перемещение ОВ относительно других элементов конструкции ОК. При этом в демпфере, ОВ и его покрытии возникают определенные напряжения, стремящиеся вернуть все точки конструкции в исходное положегше. Для расчета возникающих напряжений рассмотрим следующую модель (рис. 6.10). Каждое ОВ окружено воображаемым коаксиальным Рис. 6.10. Схема модели для расчета относительного удлинения ОВ при изгибе при его плотной укладке в конструкции ОК : / 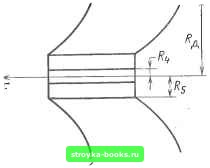 у . [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [ 43 ] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.001 |