
 |
|
Главная Развитие оптической связи [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [ 67 ] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] полученный на выходе кабеля импульс, берутся отдельные выборки, т. е. мгновенные значения импульса, и затем по определенному алгоритму для преобразования Фурье проводятся вычисления. Для существенного сокращения времени и трудоемкости операций при использовании нормированных импульсов можно применить приближенно типовые характеристики. Этот метод основан на том, что структура ОВ как направляющей системы остается одинаковой для различных образцов волокон независимо от значений их первичных параметров. Поэтому при неизменной форме входных сигналов на выходе ОК будем иметь импульсы, одинаковые по своему аналитическому описанию, отличающиеся друг от друга только значершями некоторых параметров, зависящих от первичных параметров волокна. f, Если в качестве входных импульсов выбрать импульс симметричной формы (например, приближающийся к гауссовой), то возможные формы импульсов на выходе кабеля будут приближенно, но с достаточной точностью принадлежать к некоторому семейству приближенно-типовых импульсов (ПТ-импульсов), отличающихся друг от друга только одним параметром. Эти ПТ-импульсы точно описываются следующими двумя выражениями (для двух типов импульсов): sinTie >.,= ""VigTry (10.15) О ; 00; 01; Ус = i-cos27re л Е-е\ п . тегЫ- (10.16) о ; 00; 01, где Q=t/x; t-абсолютное время; т - полная длительность импульса; Ъ,-абсцисса максимума импульса (в единицах 0). ft На рис. 10.7 и 10.8 приведены кривые, описывающие ПТ-импульсы с параметрами , равными 0,1; 0,2; 0,3; 0,4; 0,5. Кривые с параметрами =1-, т.е. 0,9; 0,8; 0,7; 0,6, не приведены, так как они идентичны по спектрам этим же кривым, но расположены симметрично (зеркально) относительно оси: 0 = 0,5 по отнощению к приведенным кривым. Для этих всех вариантов форм выходных импульсов рассчитаны нормированные частотные спектры к{у.\ К{)-> приведенные на рис. 10.9 и 10.10. Сопоставив форму экспериментально , полученного выходного импульса с наиболее близкой ему 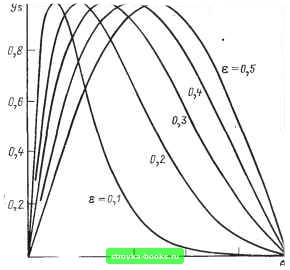 о \2 0,6 0,8 • Рис. 10.7. Приближенно-типовые импульсы формой ПТ-импульса, определим параметр и далее из рис. 10.9 или 10.10 найдем нормированный спектр. Ниже подробно описана последовательность этих операций. 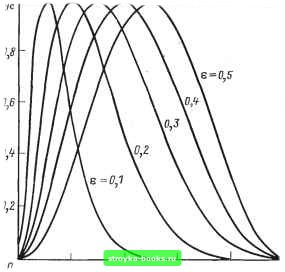 0,2 0,4- 0,6 0,8 Рис. 10.8. Приближенно-типовые импульсы 206 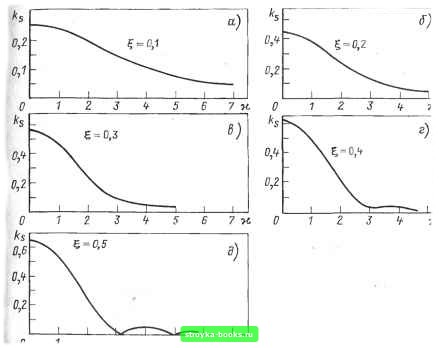 2 J Ч- 5 6 7 Н Рис. 10.9. Нормированные частотные спектры 1. Определение параметра . Экспериментально полученный импульс, зафиксированный с экрана осциллографа или переснятый на фотопленку, приводится к масштабу кривых на рис. 10.7 и 10.8. Для этого определяются отношения ?x = i:„/x„o; w/>max, где т„-ширина полученного импульса, взятая на его нулевом уровне; Smax - его максимальнос значение; т„ и s„ берутся в линейных единицах на осях координат; х„игх и Утах-максимальные значения (в линейных единицах) величин в п ys или у на рис. 10.7 и 10.8. Тогда координаты точек кривой, описывающей экспериментально полученный выходной импульс в приведенном масштабе, будут: у = дуу; x = q,.x; у, х-координаты экспериментально полученной кривой (импульса). Далее находится кривая на рис. 10.7 или 10.8, с которой наилучшим образом со-рмещается полученная в приведенном масштабе кривая. Под наилучшим совмещением имеется в виду выбор такой кривой, которая будет наиболее близка по форме к экспериментальной кривой. Дополнительным критерием наилучшего совмещения является условие, при котором при наложении экспериментальной кривой на типовую сумма площадей отклонений по обе стороны типовой кривой будет минимальной. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [ 67 ] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.0009 |