0,3 0,2

0,-Ь

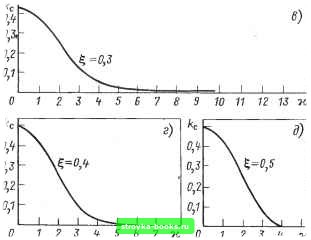Рис. 10.10. Нормированные частотные спектры

Соответственно устанавливается значение параметра для выбранной таким образом кривой (6) или у (6).

Если кривая, описывающая форму экспериментально определенного импульса, оказывается зеркальной по отнощению к кривым на рис. 10.7 или 10.8, следует кальку (или фотопленку), на которой нанесена преобразованная по масштабу кривая, расположить на рисунке своей обратной стороной симметрично относительно 6=0,5 и в таком положении найти оптимальное совмещение.

2. Определение спектра импульса. По выбранному виду функции Уз[) или Ус{) и параметру Ъ, на рис. 10.9 или 10.10

находят кривую, описывающую нормированный спектр выходного импульса А;, (к) или А; (к).

Аргумент K = Qx/n = 2F/i выбран таким образом, что нор-]У1ированный спектр приближенно-типового импульса может быть выражен так:

F=y./2x.

3. Определение амплитудно-частотной характеристики кабеля. Амплитудно-частотная характеристика может быть получена из выражений

Вье индексы «вых» и «вх» относятся к спектрам выходного

входного импульсов. Р»- Спектр входного (нормированного) импульса предполагается заданным, т. е. известным.

4. Измерение дисперсии. Дисперсия ОВ определяется его модовой структурой и частотными зависимостями коэффициента распространения и диэлектрической проницаемости материала ОВ.

Независимо от вида и характера дисперсии принято оценивать конечное проявление дисперсии по максимальному относительному запаздыванию высшей передаваемой частоты спектра сигнала на единичном пути его распространения.

Измерение дисперсии проводится в основном для одномодовых волокон, для которых эта величина дает возможность достаточно полно оценить характеристики передачи и искажения сигналов, хотя и не отражает особенности, связанные с формой входного сигнала.

Применительно к многомодовым волокнам знание дисперсии является существенно недостаточным для полного описания характеристик передачи и распространения оптических сигналов, так как дисперсия является частным параметром.

Непосредственный метод определения дисперсии сводится к измерению относительного запаздывания на пути распространения импульсов для двух значений оптических длин волн A-i и А-г.

Если x{ki) и т(А,2) представляют собой временные задержки импульсов на пути / для соответствующих длин волн, то дисперсия

Ai -Л2)1

Ik Основной проблемой является правильное измерение значения задержки. Импульсы, введенные в начало измеряемого кабеля, приходят к его концу искаженными, что создает неопределен-

ность в правильном выборе точек на кривых, описывающих импульсы, относительно которых измеряется запаздывание.

При этом следует иметь в виду, что хотя погрешности измерения времени задержки должны уменьшаться с уменьшением продолжительности импульсов и увеличением крутизны и фронтов, однако при этом степень искажений увеличивается и, в частности, увеличивается относительное уширение выходных импульсов.

Для уменьшения влияния указанных факторов на погрешность измерения времени запаздывания форма и продолжительность входных (испытательных) импульсов должны быть выбраны оптимальными.

Так как измеряется групповое время запаздывания, то точки на оси времени, между которыми следует измерять запаздывание, должны совпадать с абсциссами центров тяжести площадей, ограниченных кривыми, описывающими входной и выходной импульсы.

В этом случае искажение импульсов и их расширение на выходе не повлияют на правильность измерения запаздывания.

Абсциссы центров тяжести импульсов

+ 00

to= ] tPo{t)dt; (J0.18)

- 00

tl= j" tpl{t)dt,

- оо

где Po{t) и Pi{t)-аналитические описания формы входного и выходного импульсов. Величины to и ti определяются в той же системе отсчета, в которой описывается Po,i{t).

В качестве входного выбирается гауссовый импульс (или близкий ему по форме)

Po{t) = P,r,c-"\

в этом случае to совпадает с абсциссой максимума импульса.

Если выходной импульс сохраняет симметричную форму, то ti также соответствует его максимальному значению, и тогда запаздывание определяется интервалом между этими максимумами.

В общем случае форма выходного импульса отлична от входного и является асимметричной; при этом значение ti определяется расчетом по (10.18). Для этого находится графоаналитическое решение интеграла

l{yi)]\Pi{t)dt;

- V.

\v.\<oo принимается таким, при котором Pi{y.)<Pi{tmax), где tmax соответствует максимальному значению Pi, например, Л{к)=10-Л(г„„.).