
 |
|
Главная Среднее значение величин [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 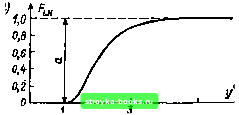 0,д 0,6 5 xiQf
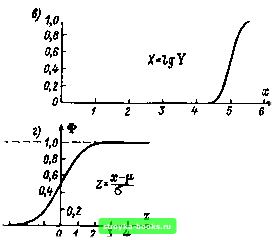 -3 -2 -1 Рис. 1.16. Преобразование логарифмически нормального распределения: а - трехпараметрическое логарифмически нормальное распределение с начальным значением а= 100 ООО; б - логарифмически нормальное распределение (а=0; (i=lg 100 000=5; a=lg 1,7783=0,25); в -нормальное распределение (Х=5; 0=0,25); г - нормированное нормальное распределение (Х = 0; 0=1) Плотность распределения (двухпараметрического): при X=\nY: уф (In г/; \i; а) (1.70) (у>0); при X = \gY: I (г/<0); In 10 ф(1§г/; o) {y>0). (1.776) функция распределения (двухпараметрическая): при X=ln Y: (О (w < 0); НфЦпу, g-) (.>0); (•«) (1.71) при X=lgy: О iy<0); (Igy; Ji; a) (t/>0). (1.786) Параметры: ц (вещественный; среднее значение преобразованной величины); (больше 0; дисперсия преобразованной величины). Математическое ожидание: при Х=1п У: £r = exp(ji+-"); (1.79а) при X=\gY: £F = exp(tilnlO-f-ln40y (1.796) Дисперсия: при Х=1п У: Dr = [ехр (а) -1 ] ехр (2ji а); (1.80а) при X=\g У: Dr = [ехр (а In Ю)-1] ехр {2\i In 10 + In 10). (1.806) Пример: рис. 1.17. В отличие от нормального распределения логарифмически нормальное распределение несимметрично; дисперсия и математическое ожидание определяются обоими параметрами ((X, а). Таблицы. Поскольку работают только с преобразованной случайной величиной, используются таблицы нормального распределения Л(0; 1) [27]. Точечные и доверительные оценки. Параметры распределения преобразованной случайной величины Х = 1пУ или X = lgY оценивают и вычисляют аналогично расчету параметров нормального распределения ц и а (см. п. 1.3.1). Применение. Это распределение первоначально использовалось в таких задачах высоковольтной техники, как определение 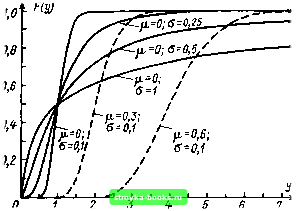 Рис. 1.17. Логарифмически нормальное распределение случайной величины У при различных значениях }х и а времени пробоя и времени жизни [44-47], в последнее время, правда, эти процессы чаще описываются распределением Вейбулла. Распределение Вейбулла и экспоненциальное распределение. Модель. Распределение Вейбулла [48] принадлежит к группе экспоненциальных распределений [49], образующихся по одной модели. В зависимости от обстоятельств случайная величина является экспериментальной величиной (максимумом или минимумом) всех возможных реализаций. Примером может служить пробой параллельных изолирующих промежутков, возникающий в случайном месте с ослабленной электрической прочностью. Уже поэтому делается ясным больщое значение экстремальных распределений (с минимальным значением) для высокочастотной техники. Для получения экстремального распределения [22, 49] рассмотрим п элементарных событий, заключающихся в возникновении случайных значений Xj, распределенных по одинаковому закону Ра{х). Рассматриваемая случайная величина X должна быть минимальной из всех возможных значений: X=min (Xj). По закону умножения (см. п. 1.1.3), или, что то же, по закону суперпозиции (см. гл. 5), для непоявления события X необходимо, чтобы Р{Х>х)==[1-Рл{х)Г, откуда для его возникновения, или, что то же, для функции распределения случайной величины X, F„ {X) = Р {Х<х) = 1 [1 f д {х)Г. (1.81) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 0.0012 |
||||||||||||||