
 |
|
Главная Среднее значение величин [0] [ 1 ] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] сов позволяет установить, с какой вероятностью на единицу времени будет освобождено заданное число начальных электронов. Последующее развитие лавины опять является случайным процессом: при ударе начальных электронов в молекулу газа образуется еще один электрон (ионизация, размножение электронов), либо он теряется (прилипание, потери электронов), или же остается неизменным (упругое соударение, число электро-
0,01 0,02 0,03 Рис. в.2. Моделирование шести лавин (/-б) электронов в однородном поле в элегазе (Р2о=ОЛ МПа; £=90 кВ/см; ге -число электронов; / - путь, пройденный лавиной) нов не меняется). В электронной лавине поэтому число электронов меняется дискретными случайными ступенями (рис. В.2), причем относительно малому числу начальных электронов может удастся образовать настолько мощную лавину («кя:; 10* носителей заряда), что произойдет пробой. Для математической формулировки проблемы используются коэффициенты ионизации и прилипания, характеризующие интенсивность образования и гибели электронов. С их помощью можно вычислить зависящую от напряженности поля и числа начальных электронов вероятность того, что будет достигнуто критическое число электронов в лавине «к. Поскольку эта вероятность должна восприниматься как вероятность пробоя, ее связь с необходимой для пробоя напряженностью поля дает чрезвычайно интересную с технической точки зрения функцию распределения пробивной напряженности пр (например, в однородном поле, рис. В.З, а). Хорошо известно, что с увеличением числа начальных электронов элемент случайности теряется. Если, как при ч) 1.0 0,8 0,6 0,2 О 85 90 S5 100 105 110 115 кВ/см 5) 0,6 0,5 0, 0,3
85 90 95 100 105 кВ/см Рис. В.З. Функция распределения напряженности пробоя в элегазе, найденная путем статистического моделирования при Р20=0,1 МПа: а - однородное поле (i -/гк=оо; 2-100; 3-10 (число начальных электронов); 4 - «„=1); б - коаксиальные цилиндры с одним начальным электроном (внутренний цилиндр с отрицательным потенциалом; радиус наружного цилиндра 5 см; штриховая линия - распределение в однородном поле) импульсном напряжении, образуется очень мало электронов, то внутренне присущая процессу случайность отчетливо выражена. Напротив, большое число начальных электронов, как при длительном приложении напряжения, приводит к детерминированному поведению процесса. (Большой разброс значений измеренного напряжения пробоя обусловлен случайными внешними условиями, например наличием пыли в системе.) В неоднородном поле на процессы образования и гибели электронов не наложено каких-либо существенных ограничений, однако для понимания процесса необходимы численные расчеты. Функция распределения максимальной пробивной напряженности электрического поля £пртах зависит, однако, от геометрии электродов (на рис. В.З, б приведен пример распределения для одного начального электрона) и по граничным значениям близка к функции распределения в однородном поле. Кроме того, имеется зависимость от полярности приложенного напряжения, поскольку от нее зависит направление развития лавины электронов. Статистическое моделирование дает возможность исследовать вероятность пробоя в зависимости от начальной точки появления начального электрона (рис. В.4). При этом очевидно, что эффект полярности пробивного напряжения должен существовать. 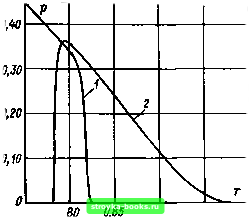 0,75 О, 0,90 0,95 см Рис. В.4. Зависимость вероятности пробоя в элегазе от места образования начального электрона и полярности внутреннего электрода (внутренний радиус коаксиального цилиндра 0,75 см, наружный - 20 см; Р20=0,1 МПа; £тах=110 кВ/см) / - отрицательная полярность; 2 - положительная полярность Обе части случайного процесса (образование одного или более начального электрона и развитие лавины), естественно, еще должны будут рассматриваться. Созданная модель чрезвычайно сложна математически, и достигнутые возможности позволяют предсказать исход процесса, правда, вполне удовлетворительно качественно, но не количественно. Поскольку для физических случайных процессов главным образом используют статистическое моделирование, дальнейшее развитие разработанных методов будет происходить в очевидном направлении туда, где находятся непосредственно требующиеся в технике результаты. Предпосылкой этого является восприятие инженерами статистических категорий. Относительно простые математически, предлагаемые в данной книге с инженерных позиций статистические оценки должны поэтому помочь дальнейшему проникновению статистических методов в электротехнику. [0] [ 1 ] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 0.0013 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||