Пример: рис. 1.20. С помощью преобразования у= {х- -ti)/y двойному экспоненциальному распределению придают стандартную форму с т1 = Хбз=0 и у=\, как показано в табл. 1.17. Квантиль порядка q двойного экспоненциального распределения в общем виде вычисляется на основе его значения для стандартной формы как

(1.97)

Точечные оценки. Параметры оцениваются одновременно с квантилями эмпирической функции распределения

(1.98) (1.99)

y* = (Авз-ДГ05)/3.

Равным образом возможна точечная оценка с помощью эмпирических моментов (1.95) и (1.96). Для получения правильной оценки при этом следует рассматривать выборки ограниченного объема. С помощью множителей kn (lim kn = V"*76 ) и

kn (lim felf* = С = 0,5772 . . .\ зависящих от объема выборки, и

ЧП-».оо У

табл. 1.18 [22, 49] получаем:

П ,= 1

(1.101)

Доверительные оценки. Доверительные оценки параметров двойного экспоненциального распределения до настоящего времени неизвестны. Указания для расчета некоторых «контрольных интервалов», которые в среднем диапазоне двойной экспоненты могут быть приняты за доверительные интервалы, имеются в работе [22].

Применение. Двойное экспоненциальное распределение с успехом применяется для описания случайных величин пробивного напряжения и электрической прочности, причем это распределение особенно эффективно для описания процессов в изоляции со сжатым газом [25]. При большом значении показателя экспоненты Вейбулла (боо) двухпараметрическое распределение Вейбулла сливается с двойным экспоненциальным распределением; уже при б>20 целесообразно использовать двойное экспоненциальное распределение. При использовании закона умножения (см. § 5.3) нормальное распределение при возрастающем коэффициенте п-оо переходит в двойное экспоненциальное распределение. Этот переход открывает дальнейшие возможности его применения.

Использованная литература: [25, 49, 75-78].

Распределение с двухсторонним ограничением (распределение Вольмута).

Модель. Неограниченность нормального распределения неудобна при решении некоторых специальных технических задач. При этом на нормальное распределение накладывают ограничения в точках Xu = \i.-kb и x = \i, + kb (чаще всего при этом k меняется от 2 до 3), или устанавливают какие-либо другие гра-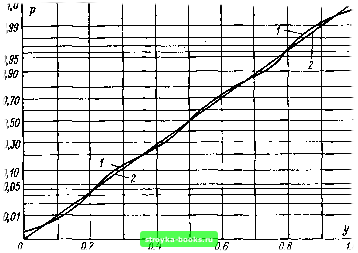

1.21. Сравнение распределения с двухсторонним ограничением Рп{у) кривая / [80] и нормального распределения [0,5; (1/6)2] -кривая 2

Вероятностная сетка распределения Fiy)

ницы [79]. Как показано в работах [56, 80], математически удобным является распределение с двухсторонним ограничением, которое в широком диапазоне очень хорошо аппроксимируется нормальным распределением, ограничено с двух сторон и имеет только два параметра (рис. 1.21). Функция распределения:

/ \ 1,635 / х~х„ 41,635

{х < Хо); (д;о<д:<Х1оо);

(х > Хюо)-

(1.102)

Параметры: Хо (начальное значение); Хюо (конечное значение).

Нормирование. При г/о = 0 и «/ioo=l

Хщ - х Хш - 0

Поскольку функция плотности симметрична относительно У = 0,5, можно табулировать Рв{у) только в диапазоне 0<«/< <0,5; 1-(г/)-в диапазоне 0,5<:г/<1 (табл. 1.19).