Главная  Среднее значение величин 

[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [ 22 ] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101]

Применение. Гамма-распределение находит применение в теории надежности; /"-распределение играет важную роль при доверительных оценках дисперсии (см. п. 1.3.2) и при тестах (см. § 1.5): х-критерий приспособляемости, х-тест независимости, х-тест рассеивания и др. [27].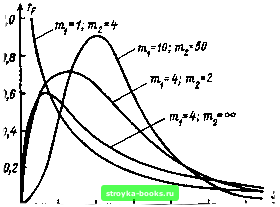


0, 0,8 1,2 1,6 2,0 2,¥

Рис. 1.23. Плотность распределения fir(je) F-распределения с тп степенями

свободы

/•-распределение.

Модель. Если F и Z - две независимые случайные величины, распределенные по закону с mi и тг степенями свободы, то частное

имеет /-распределение со степенями свободы т\ и т. Плотность распределения:

fFix) =

{х < 0);

"«1 Ч"" „m,/2-l

V «2 /

/mi Ота Л

.(1 + ;,)-<"+"=>/ (;,>0),

(1.107)

где В (г; s) = Jf- (1 - х)dx - бета функция [50]. Параметры: mi и тг - степени свободы.



функция плотности -распределения изображена на рис. 1.23.

Математическое ожидание:

£Х = тг/(7Иг-2) (7Иг>2).

Дисперсия:

2т? (от,+«2 -2)

Таблицы. Задаются важнейшие квантили для степеней свободы из диапазона l<mi<:oo, 1<т2<:оо [27, табл. 6] - табл. 1.21.

Таблица 1.21

Чнсло степеней свободы т,

Квантили f т,; mj; « F-распределения при числе степеней свободы т,, равном

6 1 8

Порядок q = 0,95

4.28

4.15

4,06

3,98

3.92

3,87

3.58 3,22

3.44

3.35

3,26

3.20

3.15

3.07

2.98

2,89

2,83

2.77

2.92

2,77

2.67

2,58

2.51

2.46

2.74

2.59

2.49

2,40

2.33

2.28

2.60

2,45

2,35

2,25

2.18

2.12

Порядок q = 0.975

5.82

5.60

5,46

5,33

5.24

5,17

4.56

4.43

4,30

4.16

4,08

4,00

4.07

3,85

3,72

3.58

3.50

3.42

3.60

3,39

3,25

3.11

3.03

2,95

3.34

3,12

2.99

2.85

2,76

2.68

3,13

2,91

2,77

2,64

2.55

2,46

Применение. Распределение F играет важную роль в статистических тестах (см. п. 1.5.2): при сравнении дисперсий (f-тест), дисперсионном анализе, сравнении средних величин и т. д. [27].

-распределение.

Модель. Если Y и Z - независимые случайные величины, величина У распределена нормально как iV (0; 1), а Z имеет х-распределение с т степенями свободы, то отношение Х=У1л111т обладает распределением с т=1 степенями свободы. Кроме того, отношение двух независимых нормально рас-



771=*

/0,2

0,1

-/ D

Рис. 1.24. Плотность распределения ]t(.x) -распределения с т степенями

свободы

пределенных iV(0; 1) случайных величин обладает -распреде-лением с числом степеней свободы т=\. Плотность распределения:

Г (от/2) л/шп

\-<m-f-l)/2

(1.108)

Параметр: т - число степеней свободы.

Поскольку /-распределение симметрично и неограниченно, при т-оо оно переходит в нормальное распределение iV(0; 1) (рис. 1.24).

Математическое ожидание:

Дисперсия:

£Х = 0 (т>1).

от -

(т>2).

Таблицы. Задаются важнейшие квантили tm;q pacпpeдeлe-ния для 1<т<оо [27, табл. 5] - табл. 1.22; ввиду симметрии

функции распределения tm;l-q = -tm;q.

Применение, /-распределение играет важную роль при доверительных оценках и тестах: доверительных оценках средних величин (см. п. 1.3.2), регрессионном анализе (см. п. 1.4.3), сравнении средних величин (см. п. 1.5.2), проверках на независимость и др. [27].



[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [ 22 ] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101]

0.0011