1.3.3. Суперпозиция распределения. Многие эмпирически получаемые функции распределения представляют собой наложение двух или нескольких теоретических функций

Пример 1.24. Рассматривается пробивное напряжение в горизонтально расположенном коаксиальном кабеле с элегазовой изоляцией, в котором имеется дефект в виде свободно перемещающейся частички.

При постоянном напряжении частичка движется и, когда она приближается к внутреннему электроду, происходит пробой. Инициированный частицей пробой при постоянном напряжении распределен по нормальному закону [рис. 1.25. f (Ипр. пост)]. При импульсах коммутационных перенапряжений частичка не перемещается, пробой является следствием возмущения поля и пробивное напряжение выше, чем при постоянном напряжении. Функция распределения пробивного напряжения при нмцульсах коммутационных перенапряжений опять аппроксимируется нормальным распределением [рис. 1.25; f(Unp. ком)]. При наложении постоянного напряжения и импульсов коммутационных перенапряжений процесс пробоя в каждый момент определяется суммарным напряжением. Если частица случайно окажется в своем движении под действием постоянного напряжения вблизи внутреннего электрода, то пробой произойдет, как при постоянном напряжении; если частица будет оставаться вблизи наружного электрода, то пробой произойдет, как при импульсах коммутационных перенапряжений.

В результате такого наложения функция распределения представляет собой суперпозицию двух распределений [рис. 1.25, f(u„p. см)]. В определенных случаях возникают распределения, способные описать процессы, при которых в изолирующей конструкции пробой может иметь место без частичных разрядов и с частичными разрядами нли когда пробою предшествуют различные формы частичных разрядов.

Физической причиной возникновения подобных суммарных результирующих законов распределения

при Z 1

(1.109)

См. также Г. С. Кучинский. Частичные разряды в высоковольтных конструкциях.- Л.: Энергия, 1979. {Прим. перев.)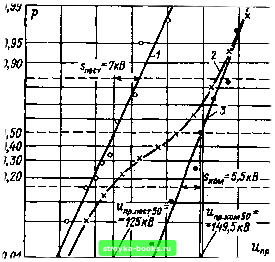

0,10 0,05

100 110

150 160 кВ

Рис. 1.25. Пример суперпозиции распределений

Пробой промежутка между коаксиальными цилиндрами в элегазе; / - функция распределения при постоянном напряжении f ("пр. пост 2 - функция распределения при суперпозиции f ("пр. см- - функция распределения при коммутационных перенапряжениях PjUjjp комм вероятностная сетка нормального распределения

ЯВЛЯЮТСЯ различные механизмы [описываемые различными функциями распределения Fi{x)], под действием которых может образовываться результирующий процесс, описываемый функцией распределения F{x).

Наряду с такими «суммарными» сложными распределениями часто говорят о «перемножаемых» [69]. Это относится к применению распределения Вейбулла (см. п. 1.3.2) в описанных моделях («пробой в слабонеоднородном поле»), основанном на законе перемножения вероятностей. Перемножаемые сложные распределения образуются в случае, применения закона перемножения (см. § 5.3 и 5.4).

Рассматриваемые суммируемые сложные распределения [26, 40, 69, 81-83] чрезвычайно трудно изучить математически. Расчетная обработка распределения двух нормальных распределений связана уже с рассмотрением пяти параметров 6i, Jill, an, a), является чрезвычайно сложной и приводит к большим погрешностям. При этом остается эмпирический путь, основанный либо на использовании аналоговых вычислительных

Параметр а в соответствии с выражением (1.109) задает ai=a и ап-= 1-а.

машин [40], либо просто на графической обработке с помощью вероятностной сетки [81, 84, 85]. При графической обработке исходят из эмпирической функции плотности распределения f*ix), которую интуитивно заменяют функцией плотности Fi*{x) определенного типа распределений, после чего в результате наложения Fi*{x) вновь переходят к исходной плотности f*{x). Эта процедура облегчается в том случае, например, когда при использовании вероятностной сетки нормального распределения внешний вид эмпирической функции плотности F*(x) стремится к прямым линиям, если обе суммируемые функции плотности fi*ix) нормальны. При графической обработке следует исходить из этих прямолинейных ветвей.

Пример 1.25. Сложное распределение из примера 1.24 необходимо разложить иа составные части (рис. 1.25). Поведение сложной функции f («пр. см) и описываемая модель наводят на мысль, что f (Ипр. см) состоит из двух нормальных распределений. Для получения эмпирической плотности распределения данные измерений должны быть сведены в таблицу (см. п. 1.2.2) и обработаны (табл. 1.23, объем выборки п=199). Эмпирическая функция распределения изображается графически (рис. 1.26) и интуитивно делится на два слагаемых.

В таблице указывается эмпирическая частость каждого слагаемого. Сумма этих частостей задает теперь уже параметры ai = 0,42=a и аи = =0,58=1-0. Для графического определения параметров как квантилей

Таблица 1.23

Границы интервала

"npfeH

"npfeB

Частость

абсолютная

относительная

о it

Относительная частость в подмножестве

Относительная суммарная

частость в подмножестве

"Ski

1 2 3 4 5 6 7 8 9 10 11 12

107,5 112,5 117,5 122,5 127,5 132,5 137,5 142,5 147,5 152,5 157,5 162,5

112,5 117,5 122,5 127,5 132,5 137,5 142,5 147,5 152,5 157,5 162,5 167,5

2 4 12 20 19 15 20 28 34 26 11 2

0,010 0,050 0,120 0,220 0,315 0,390 0,490 0,630 0,800 0,930 0,985 0,995

0,010 0,040 0,070 0,100 0,095 0,075 0,100 0,140 0,170 0,130 0,055 0,010

0,010 0,040 0,070 0,100 0,093 0,062 0,032 0,010 0,002

0,002 0,013 0,068 0,130 0,168 0,130 0,055 0,010

0,995

= 0,419 а » 0,42

= 0,576 1 -а » »0,58

0,024 0,119 0,286 0,525 0,747 0,895 0,971 0,995 0,999

0,003 0,026 0,144 0,370 0,662 0,888 0,983 0,999