
 |
|
Главная Среднее значение величин [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [ 24 ] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 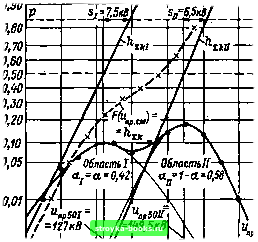 0,001 105 115 125 155 П5 155 185 кВ Рис. 1.26. Разложение сложного распределения f («др. сн), изображенного на рис. 1.25 («пр 501, Si, Ипр 50/7, sii) следует для каждого слагаемого получить суммарные частости 1 * "л /=1 в результате будет найдена следующая сумма двух нормальных распределений: F (Ипр. с«) = 0,42Ф (Ипр; 127 кВ; (7,5 кВ)») + 0,58Ф («пр; 149,5 кВ; (6,5 кВ)). Параметры распределений-слагаемых хорошо совпадают с параметрами функции распределения при постоянном напряжении и при импульсах коммутационных перенапряжений (рис. 1.25 и 1.26). Из-за связанных со сложной функцией распределения математических трудностей ее следует использовать лишь тогда, когда к ней приводит физическая модель, например подобная описанной в примере 1.24. Ни в коем случае не следует пытаться определять по сложному распределению эмпирических взаимосвязей без такой модели. Несомненно, что сложные функции распределения образуются при суперпозиции многочисленных взаимосвязей в природе и технике, однако в конечном итоге в интересующем диапазоне преобладают отдельные влияния, рассмотрение которых для техники оказывается достаточным. Например, при использовании закона умножения (см. гл. 5) для сложной функции распределения из примера 1.25 следует рассматривать одно нормальное распределение, найденное для области I. 1.4. Основы теории корреляции и регрессионного анализа 1.4.1. Определения и принципы. Если при испытаниях одновременно измеряются несколько случайных характеристик (например, интенсивность частичных разрядов при известном испытательном напряжении и уровень пробивного напряжения), то представляет интерес, связаны ли между собой эти характеристики, насколько сильна эта связь и как ее математически сформулировать. Понятия корреляции и регрессии дают ответ на эти вопросы [17]. Корреляционный анализ в первую очередь исследует вопрос, ие является ли взаимосвязь между изучаемыми случайными характеристиками X а Y линейной и описывает уровень этой связи коэффициентом корреляции р. Пусть случайные величины X и Y распределены по нормальному закону. Коэффициент корреляции может принимать значения р < 1. Величины X и У будут некоррелированы, если р = 0 (рис. 1.27,а, б), что означает отсутствие линейной связи между ними. Чем ближе р к единице, тем сильнее выражена корреляция. При р>0 величины X и Y одновременно увеличиваются или уменьшаются; тогда говорят о положительной корреляции (рис. 1.27, в). При р<0 увеличение X связано с уменьшением Y и имеет место отрицательная корреляция (рис. 1.27,г). При р = 1 имеет место полная корреляция, что означает прямую функциональную зависимость (рис. 1.27, д). Определение оценки г для коэффициента корреляции р по выборке п пар величин (Xi; ус) будет описано в разделе 1.4.2. Регрессионный анализ по выборке устанавливает возможность существования функциональной взаимосвязи, с одной стороны, между двумя случайными величинами X и У, а с другой - между случайными величинами и параметрами (например, зависимость предпробойного времени от приложенного напряжения). Изложенные проблемы математически формально решаются одинаково. В простейшем варианте при регрессии графически изображают пары (л;,; уг) {Xi являются, к примеру.  Рис. 1.27. Изображения реализаций случайных величин X и У (схема): а - корреляция отсутствует (р=0); б -линейная корреляция отсутствует (р=0); в - положительная корреляция (0<р<1); г - отрицательная корреляция (-1<р<0); й -полная корреляция (функциональная взаимосвязь) (р=1) параметром, уг - реализацией случайной величины). При этом должен рассматриваться лишь случай линейной взаимосвязи между характеристиками X и Y или приводящейся к линейной путем простых преобразований: X*=fi{X) и У*=/2 (У) (линейная регрессия). Пример 1.26. При исследовании связи между приложенным напряжением «пр и временем до пробоя tnj> высокополнмерной изоляции имеет место линейное соотношение между их логарифмами в форме Ig "пр =--- Ig пр + Ig "пр о (закон длительности жизни). Выполняя измерения, используют линейную регрессию между величинами lg"np и Ignp. При линейной регрессии нормально распределенные случайные величины связываются линейной функцией. Прямая регрессии изображает математические ожидания как EY = a + EX; Y = a + X. (1.П1) В простейшем случае ее проводят по выборке таким образом, чтобы графические изображения пар величин {xt; yi) были разделены примерно поровну (рис. 1.28). Если имеются точные значения, то по методу наименьших квадратов должны быть вычислены оценочные значения коэффициентов а и р (а; Ь) (коэффициенты регрессии) (см. п. 1.4.3). Если разброс реализаций велик, а наклон прямой регрессии и коэффициент регрессии мал,,то имеет место слабая линейная взаимосвязь между величинами X VI Y (рис. 1.28,а). Если разброс, напротив, мал и коэффициент р велик, то ясно видна сильная взаимосвязь (рис. 1.28, б). По этому признаку разделяют зависимые и неза- 1 р-шло; $-6елико % L Велико; s-мало Рис. 1.28. Изображения реализаций случайных величии X и У прн различной степени взаимной зависимости (схема): а -слабая зависимость; б - сильная зависимость (Р - коэффициент регрессии; s -разброс) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [ 24 ] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 0.0013 |