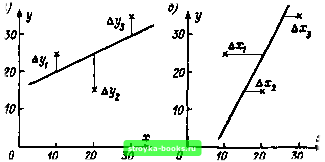Рнс. 1.29. Смена зависимой н независимой переменной прн регрессионном анализе: а - регрессия (/по.«(2(Д(/()2=min); б - регрессия х по 1/(2(Дх<2) =

=min)

висимые характеристики (параметры). При оценке зависимости у от X эмпирическая прямая регрессии

(1.112)

является оптимальной аппроксимацией эмпирически определенной величины у (рис. 1.29,а). При этом минимальной будет сумма вертикальных отклонений, в то время как в противоположном случае

х = а,у + ЬуУ (1.113)

минимальна будет сумма горизонтальных отклонений (рис. 1.29,6). Какую регрессию следует выполнять, зависит от конкретных условий. При увеличении корреляции разница между прямыми регрессии (1.112) и (1.113) уменьшается (рис. 1.30). При коэффициенте корреляции " = 1 обе регрессии совпадают и для коэффициентов регрессии имеет место

b,y=Vby,, (1.114)

Рнс. 1.30. Взаимосвязь между прямыми регрессии х по у (или у т х) и коэффициентом корреляцин г (схема) прн г=0 (а), 0<г<1 (б) н г=1 (в)

в то время как в общем случае (г<1)

(1.115)

Ниже будет показано, как определяются коэффициенты корреляции и регрессии в простейшем линейном случае. Специальная литература по статистике предлагает инженерам обширный материал для многих других случаев [17, 18, 22, 26, 82, 83].

1.4.2. Оценка коэффициента корреляции. Пусть имеется выборка п пар данных (jCi; t/<) Для ее описания вычисляются средние арифметические х vi у (см. выражение (1.41)] и средние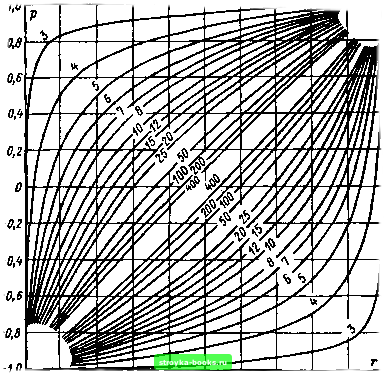

-1,0 -0,8 -0,6 -0,4 -о,г

0,2 0,4 0,6 0,8 1,0

Рис. 1.31. Двухсторонние доверительные интервалы для коэффициента корреляции с доверительной вероятностью е=0,95 в зависимости от объема выборки п

квадрэтические отклонения Sx и Sy [см. (1.48)]. Их дополняет эмпирический коэффициент ковариации

1 - -

Sxy=-- Z {Xi-X){yiy),

n-1 ,=1

(1.116)

связывающий обе величины и являющийся усредненным произведением отклонения от средних величин.

С помощью этой величины определяется эмпирический коэффициент корреляции

r = sj{sy) (1.117а)

или

r=txiyi-nxylJ[t Xi-n7)[t/-n7) . (1.1176)

как его удобнее вычислять.

В соответствии с предложенным в работе f83] (рис. 1.31) может быть определен двухсторонний доверительный интервал для коэффициента корреляции г. Поскольку для р = 0 доверительных интервалов не существует, он может быть использован лишь при наличии корреляции с р=70. Сравнение коэффициентов корреляции из различных выборок приведено в работе [18].

Пример 1.27. При определении интенсивности частичных разрядов (импульсных зарядов (7имл) при испытательном напряжении иисп=50 кВ и пробивного напряжения «пр при десяти подъемах напряжения должно быть определено, разрушается ли изоляция под действием частичных разрядов. Графическое изображение измеренных величин (рнс. 1.32) не дает ясного ответа. Для ответа поэтому следует вычислить коэффициент корреляцин и его доверительный интервал в предположении о нормальном законе распределения.

Определяют: (7нмп=34,5 пКл; иир=98,6 кВ; s,=26,0 пКл; Su=6,l кВ;

коэффициент ковариации s«u=-

85 90 95 100 105 кВ

= 85,4 кВ-пКл.

Отсюда коэффициент корреляции

г =-«==0,54. 26,0-6,1

С помощью рис. 1.31 определяем доверительный диапазон [gh= = -0,12; gb = -t-0,84]. Прн этом до-Рис. 1.32. Графическое изображение реализации случайных величин из примера 1.27 и возможные прямые регрессии

Регрессия Я,„ по и „р -сплошная линия; регрессия "пр имп ~ "Р""" линия