для коэффициента регрессии byx - cw. (1.127): [0,421; 0,821]. В особенности интересно, что параметры нормального распределения легко вычисляются по коэффициентам прямой регрессии: для Xio=x(y!f=Q)

Xso = "пр 50 = - ay J Ьух, (1.128)

для Xu=X(llf = l)

Xs* = "пр 84 = (1 - ayxVbyx, для эмпирического относительного среднего квадратического отклонения s = Xu-Xm=Vbyx. (1.129)

В данном примере найдем для параметров искомого нормального распределения: «пр 50=60,2 кВ и 5=1,6 кВ.

Изображенная на рнс. 1.33,6 прямая регрессии и оценка ее параметров являются наиболее надежными оценками, возможными при заданных т=5 точках измерений. Несмотря на чрезвычайно малый объем выборки, корреляция очевидна и показана очень наглядно. Естественно, что доверительные интервалы для коэффициентов прямой регрессии очень велики.

1.5. Проверка истинности гипотез

Статистическим тестом [17] является процедура, с помощью которой проверяют, является предположение или утверждение о (полностью или частично) неизвестной функции распределения вероятностей согласующимся с полученной конкретной выборкой или принятое распределение отклоняется от имеющегося распределения существенно, т. е. статистически значимо. Сделанное допущение является при этом статистической гипотезой, математическая формулировка которой выражается с помощью так называемой нулевой гипотезы Яо. (Альтернативная гипотеза Н\ в противоположность нулевой гипотезе отражает различие их поведения.)

Выдвинув, например, статистическую гипотезу о том, что среднее значение ц какого-либо распределения равно принятой (или заданной) величине цо, получаем нулевую гипотезу Яо: р, = цо. (Напротив, альтернативная гипотеза о том, что среднее значение ц данного распределения больще, чем р,о, должна быть выражена как Hi: р,>р,о.)

Процедура выполнения статистического теста без рассмотрения альтернативной гипотезы - так называемая проверка на значимость - состоит из четырех характерных последовательных действий:

1. Выдвижение гипотезы Яо.

В дальнейщем обсуждаются гипотезы, например, относительно типа рассматриваемой функции распределения (см. п. 1.5.1), относительно принадлежности выборки к генеральной совокупности (см. п. 1.5.2), а также относительно случайности (и в особенности независимости) получения данной выборки (см. п. 1.5.3).

2. Разработка критерия Т.

Для дальнейшего выполнения теста выдвигают подходящий критерий, основанный на преобразовании выборки. Это некоторая (случайная) функция выборки, распределение которой известно, если справедлива нулевая гипотеза Яо. Для какой-либо конкретной выборки задается соответствующая реализация теста t.

3. Определение критических диапазонов К (или критических величин ka).

Критический диапазон является частью области изменения теста Т, внутрь которого с вероятностью не больше чем а попадает реализация теста Но при условии справедливости гипотезы Яо- При этом а называют уровнем значимости, который должен быть выбран в соответствии с конкретной постановкой вопроса (обычно выбирают а<0,1; чаще всего а=0,05 или а=0,01). В зависимости от выбранного уровня значимости при помощи критической величины задаются границы критического диапазона, например: K = (kai; оо) или /С = (оо; ka) - при одностороннем тесте (рис. 1.34, а) или /С = [( - оо; кая); {кв.

Критический диапазон

Критический диапазон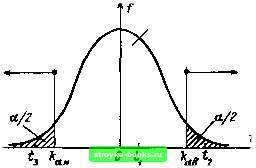

Рнс. 1.34. Иллюстрация к использованию одностороннего (а) и двухстороннего (б) тестов

Значение теста U: гипотеза не отвергается; значения тестов t, h: гипотеза отвергается; *а *ав *аи ~ критические значения; а - уровень значимости