Для выполнения графической проверки эмпирическую функцию распределения (лучше всего - полигон суммарной частости) изображают на вероятностной сетке того теоретического распределения, на основании которого должна быть выполнена проверка. Далее по реализации проводят аппроксимирующую прямую - либо произвольно, либо с помощью точечной оценки параметров, т. е. линейной регрессии (см. пп. 1.3.2 и 1.4.3). Отклонения оцениваются либо визуально, что означает использование грубого количественного критерия, либо сравнивается с границами доверительных интервалов (см. п. 1.3.2). Количественная оценка выполняется также, если для суммарной частоты задан доверительный диапазон: гипотеза относительно типа функции распределения не может быть принята, если аппроксимирующая прямая выходит за все доверительные области (рис. 1.37).

Если тип функции распределения неясен, необходимо выполнить изображение на различных вероятностных сетках.

Рис. 1.37. Графическая проверка гипотезы о применимости нормального распределения с помощью доверительных интервалов

Заштрихован диапазон возможных прямых; доверительный интервал 7: проверка ие отвергает гипотезу; доверительный интервал 7а (вместо 7): гипотеза отвергается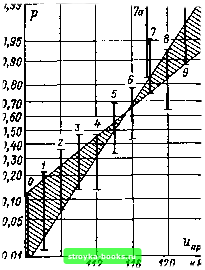

ф0,99

0,95 0,90

OfiO 0,70 0,60 0,50 0,W 0,30

0,20

0,10 0,05

0,01

0,99

0,90 0,80 0,70 0.80 0,50

0,30 0,20

0,10

0,05

0,01

6j0,99

0,95

0,90

0,80 0,W 0,60 0,50 0,40 0,30 0,20

0,10 0,05

180 200

m 200 kb

0,01

0,99

0,90 0.80 0,70

0,W 0,30

0,20 0,10 0,05

0,01

180 200

200 kB

Phc. 1.38. Графический контроль таблицы распределения из примера 1.12 с помощью вероятностных сеток: а - для нормального распределения (ипрбо= =201 кВ; 5=10 кВ); б - для логарифмического нормального распределения (дг5о=2,302; s=0,020); в -для двойного экспоненциального распределения («пр63=206 кВ; Y=9 кВ); г -для распределения Вейбулла («про=0;

«пр 63=206 кВ; 6=22,5)

Пример 1.31. Для выборки из задачи 12 (первичная таблица распределения, табл. 1.2) необходимо установить, какая теоретическая функция распределения наилучшим образом описывает эмпирические данные. Для этого полигон суммарной частости был нанесен на вероятностные сетки нормального (рис. 1.38, а), логарнфмнческн-нормального (рнс. 1.38, б), двойного

экспоненциального (рис. 1.38, в) и двухпараметрического вейбулловского (рис. 1.38, г) распределений и произвольно проведены аппроксимирующие прямые. Установлено, что лучше всего получается аппроксимация при двойном экспоненциальном распределении. При этом максимальное расхождение между полигоном и сглаживающей прямой dmax = 0,08, для распределения Вейбулла -аГтах = 0,09, для нормального распределения - dmax=0,14, для логарифмически-нормального - dmax = 0,17. К тому же двойное экспоненциальное распределение дает наилучшую аппроксимацию в диапазоне «малых» квантилей, представляющем наибольший интерес применительно к высоковольтной технике для определения выдерживаемого напряжения (см. п. 2.4.2) и закона умножения (см. гл. 5). Для приближенных качественных оценок в целом графический метод представляет большое удобство.

При малых объемах выборки (5<п<20) при проверке нормального распределения для сокращения расчетов можно отказаться от вероятностной сетки, если имеется шаблон Муртина «Минилот». С помощью этого шаблона находят реализации, соответствующие данной ординате вероятностной сетки, причем определяется уже относительная суммарная частость.

Все вероятностные сетки дают возможность выполнить прямую оценку параметров по графическому изображению с помощью метода квантилей. Необходимые для этого неизвестные квантили определяются по эмпирической функции распределения при любом типе распределения (см. п. 1.3.2).

Расчетный способ.

При расчетной проверке аппроксимации эмпирической функции распределения какой-либо теоретической последовательно выполняются описанные выше действия (выдвижение гипотезы, теста, критической величины, сравнение). В дальнейшем основное внимание уделено тесту Колмогорова [17, 27, 83 и др.], при котором оценивается максимальное отклонение эмпирического и теоретического распределений. Применяемый иногда тест Пирсона, учитывающий все отклонения при построении критерия, здесь лишь упомянут. Он подробно описан в литературе [18, 27, 83].

Тест Колмогорова.

Гипотеза. Для заданной выборки объема п неизвестная (эмпирическая) функция распределения Fn{x) сопоставляется с ожидаемой теоретической функцией распределения Fo (х).

Величина критерия. Критерием является максимальное отклонение между эмпирической и теоретической величинами:

dmax=:maK\F„{x)-Foix)\ (-oo<x<-fоо), (1.130)

как поясняет рис. 1.38.

Значение критерия можно определять графически (см. рис. 1.38), что удобно связывать с графическим тестом, или с помощью точечной оценки параметров Fo{x) в форме таблицы максимальных отклонений (путем дополнения таблицы