(!„. а для уровня значимости а, равного

ИСХОДНЫХ реализаций всеми отклонениями между эмпирической и теоретической суммарными частостями в точках реализаций).

Критическая величина. Критическая величина для двухстороннего теста табулирована ([27, табл. 19], частично - в табл. 1.26).

Сравнение. Гипотеза отклоняется, если UmaxKn;a-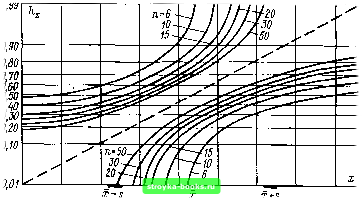

Рис. 1.39. Границы приемлемых значений теста Колмогорова [34] (уровень-значимости а=0,10)

Проблемы. Значение теста kn;a с одной стороны существенно зависит от объема выборки, и при малом объеме выборки тест не является точным. С другой стороны, особенно при графическом изображении значения теста (рис. 1.39 - «границы Колмогорова») оказывается, что оценка типа распределения в диапазоне «малых» и «больших» квантилей требует чрезвычайно большого объема выборки, что, как правило, не может быть реализовано в высоковольтной технике. Рекомендуется также увязывать выполнение теста с графическим изображением (рис. 1.38), чтобы уменьшить число точек, требующих внимания. Для сравнения различных данных можно получить сумму отклонений между эмпирическими и теоретическими величинами (или сумму их квадратов) в диапазоне рро (например, ро = 0,1).

Пример 1.32. Необходимо оценить расхождение между эмпирической и теоретической функцией распределения из примера 1.31 (рис. 1.38) с помощью критерия Колмогорова. При уровне значимости а=0,10 для выборки с п=24 табл. 1.26 дает критическое значение 24, o,io=0,242. Все отклонения меньше этого значения, и таким образом гипотеза о соответствии не отвергается. Эта проверка является недостаточно полной, чтобы отвечать той же постановке вопроса при лучшей аппроксимации. Для повышения надежности необходимо увеличить объем экспериментальной выборки л. Если такой же полигон построен прн л=100 реализациях, то при feioo; o,io=0,121 гипотеза о нормальном распределении (dmax=0,14) или логарифмически-нормальном (dfmax=0,17) определенно отвергается. Оба экстремальных распределения значительно лучше описывают имеющиеся соответствия (dmах = 0,08 нли 0,09).

1.5.2. Проверка принадлежности выборки генеральной совокупности. Часто необходимо выполнить сравнение выборок, для того чтобы принять решение о возможности объединения отдельных выборок в одну большую выборку, определить влияние определенного экспериментального параметра или выявить наличие изменений в ходе выполнения эксперимента (см. п. 1.5.3). Такое сопоставление, с одной стороны, может быть выполнено при известной зависимости функции распределения от ее параметров (параметрический тест, проверка гипотезы относительно определенного параметра), а с другой -с помощью критериальной величины как характерного признака объединенной выборки при неизвестной функции распределения (свободнораспределенный или непараметрический тест, например ранговый тест, а также U-тест).

Существует большое количество тестов [27 и 83], с помощью которых проблема может быть решена. Здесь могут быть обсуждены лишь несколько выбранных тестов, которые сведены в табл. 1.27-1.31, позволяющие систематизировать проблему,

Объединенная выборка составляется путем объединения всех сравниваемых выборок.

сослаться на возможные тесты и на литературу с примерами применительно к высоковольтной технике:

табл. 1.27 -сравнение двух независимых выборок или выборки с известной генеральной совокупностью при непрерывных случайных величинах (параметрический и непараметрический тест);

табл. 1.28 - сопоставление более чем двух независимых выборок при непрерывных случайных величинах ( = 2 -см. в табл. 1.27);

табл. 1.29 - сравнение объединенных выборок; такие выборки возникают, например, когда одинаковые серии измерений получены до и после какого-либо определенного действия (например, нагревания или длительной выдержки под напряжением), так что в каждом испытании получена одна пара реализаций; тест устанавливает влияние обработки;

табл. 1.30 - сопоставление относительных частостей и эмпирических параметров функций распределения дискретных случайных величин;

табл. 1.31 - тесты корреляции и регрессии. Параметрические тесты особенно развиты для нормального распределения. При обсуждении усредненной тенденции, однако, эти тесты можно использовать в центральном диапазоне и других распределений, поскольку в диапазоне X5o±s имеются лишь весьма незначительные расхождения между различными распределениями (рис. 1.36). Ниже приведены два параметрических теста и один непараметрический тест для сравнения двух выборок из постоянной генеральной совокупности, а также тест сопоставления двух вероятностей.

F-тест (сопоставление двух эмпирических дисперсий) [18, 27, 83].

Гипотеза. Дисперсии и Оу двух генеральных совокупностей с нормальным распределением, представленных двумя выборками объемом Пх и Пу и эмпирическими дисперсиями s,v и Sy2, идентичны: о = Оу.

Значение теста:

t = sWy (1.131)

причем при обозначении выборок следует установить s.s.

Критическое значение. Критическое значение Рщ-, т, q задается -распределением (табл. 1.21) как квантиль при числе степеней свободы mi = «,v-1; т2 = Пу-\ порядка .q=l-a/2 (двухсторонний тест с уровнем значимости а).

Сравнение. Гипотеза отвергается, если t>Fm,m;q-

Пример 1.33. Имеются две выборки значений пробивного напряжения объемом Л1 = 17 и Л2 = 21 и их эмпирические дисперсии 51=63,68 кВ и S2 = 32,60 кВ2. Поскольку Sl2>S2, обозначим s,=sД 52 = 5/; ni = /lx; П2= = Пу. В соответствии с выражением (1.131) значение теста /=1,95. Если