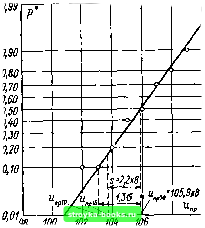108 кВ

Рис. 2.2. Изображение функции поведения иа вероятностнойч;етке нормального распределения (схема соответствует рнс. 2.1; вместо 1,3а откладывается 1,3s)

рис. 2.1 случая т=8 уровней напряжения, позволяет установить, что функция поведения, как и эмпирическая функция распределения может быть аппроксимирована нормальным распределением. Его параметры могут быть найдены как квантили (см. п. 1.3.2) нли с помощью линейной регрессии (см. пример 1.29).

Использование в практике измерений результатов экспериментов с неизменным напряжением не представляет затруднений. Их реализация, однако, затруднена как по техническим, так и по экономическим причинам, поскольку напряжение нарастает не мгновенно, но достаточно медленно (постоянное и переменное напряжение), а испытания дороги. В данных испытаниях часто желательно получить точную информацию лишь относительно того, имеет ли место решение типа «да» или «нет». В этом случае в течение опыта напряжение поднимают определенным образом вплоть до пробоя. При этом может быть использовано как непрерывно возрастающее постоянное напряжение, так и непрерывно увеличивающееся переменное напряжение с заданной амплитудой, или импульсное напряжение, увеличивающееся на величину Ди после каждого приложения напряжения (рис. 2.3). Пробой при этом является вполне достоверным событием, случайным является значение пробивного напряжения (или какая-либо полученная на ее основе величина). Подобный «опыт с подъемом напряжения», состоящий из последовательного увеличения напряжения, дает выборку из п реализаций требуемой возрастающей случайной величины. Оценка этой выборки делается точно так же, как это описано в пп. 1.2.2 и 1.5.1), и приводит к эмпирической функции распределения, которая в отличие от функции поведения будет обозначаться как «функция суммарной частости» [39, 43, 89, 90] (рис. 2.4). Разумеется, здесь уже отмечалось, что параметры опытов с нарастанием напряжения (скорость нарастания напряжения у„ или величина ступени Ди, начальное напряжение Ио) оказывают влияние на поведение функции суммарной частости. Опыт с нарастанием напряжения по сравнению с опытом с неизменным напряжением требует меньшего числа нагружений, приводящих к пробою (по сравнению с 37 пробоями на рис. 2.1 имеет место 9 пробоев на рис. 2.3), и

110 108 106

102 100 98 96 94

д. Импульсы fL без пробоя 1,

Импульсы с пробоем

4. 1

Номер cepuu.j г

Число пробоеб

6 серии... 1 1

mS...0,6 0,2 0,9 0,5 0,1 0,7 0,3 0,4-

Обще число

пробоев..- 7 2

4 5

0,8 9

Рис. 2.3. Последовательность выполнения опытов с нарастающим напряжением при импульсном напряжении и установленном начальном значении ио

(схема)

дает больше информации, хотя результат зависит от параметров эксперимента и не может быть перенесен немедленно в практическую эксплуатацию изоляции. Необходимо поэтому предварительно рассмотреть свойства функции поведения и функции суммарной частости.

2.1.2. Функция поведения и функция суммарной частости.

Монотонное увеличение функции поведения от нуля до единицы, как это изображено на рис. 2.2, необязательно. Возможно, например, что при данном межэлектродном промежутке в каком-либо газе (в так называемом аномальном диапазоне- для промежутков стержень - плоскость или

Рис. 2.4. Изображение функции суммарной частоты hz на вероятностной сетке нормального распределения (схема соответствует рис. 2.3)

0,99

0,90

0,80 0,70 0,60 0,50 0,40 0,30

0,20 0,10

0,01

98 100 102 104 106 108 кВ

0,6 0,4-

20 W

Рис. 2.5. Эмпирическая функция поведения, которую нельзя аппроксимировать какой-либо теоретической функцией распределения [93]

Коаксиальные цилиндры в воздухе диаметром 7,5 и 90 мм; импульсы коммутационных перенапряжений -f 190/18 600

60 во ЮО кВ

между коаксиальными цилиндрами в воздухе при расстояниях в несколько сантиметров [91, 92] пробой наступает при пониженном напряжении в форме стримерного разряда и при повышенном напряжении- как разряд по поверхности. Это изменение в механизме пробоя, зависящее от напряжения, приведет к тому, что по мере увеличения напряжения вероятность пробоя вначале уменьшается, а затем вновь возрастает. Подобные результаты приводятся, например, Раскиным [93] (рис. 2.5), однако это отклонение от монотонного роста не следует рассматривать как типичное для функции поведения. В большинстве случаев в относительно узком диапазоне различий в реализациях зависящей от напряжения смены механизма разряда не возникает. При этом большинство функций поведения монотонно возрастает, как и функция распределения (рис. 2.2). Нет никаких сомнений, что функцию поведения можно аппроксимировать функциями распределения непрерывных случайных величин (п. 1.3.2) и обрабатывать их так же, как функции распределения (см. § 2.2). Если возникает подозрение, что функция поведе- Qgg ния возрастает не моно- тонно, это следует проверять с помощью доверительных оценок вероятности пробоя (рис. 2.6). Если это подозрение подтверждается, то, естественно, аппроксимацию функций распределения выполнить невозможно. В этих редких случаях следует работать в даль-

Рис. 2,6. Обработка функции поведения (схема)

/ - аппроксимация функцией распределения возможна; 2 - аппроксимация функцией распределения затруднительна

0,95

0,90

0,80

0,70 0,60 0,50 Q,W 0,30 0,20

0,10 0,05

0,01

I I,