нейшем с полученной эмпирической функцией поведения. Если для какого-либо определенного импульсного напряжения (или для постоянного или переменного напряжения) заданной величины и длительности функция поведения V(Uap) данного изолятора известна, то, следуя Тетзнеру [94], можно вычислить и функцию суммарной частости для любой ступени Аи (см. также [39]).

Вероятность того, что пробой возникает при исходном значении напряжения «о, определяется прямо по функции поведения как Po=V(«o)- Вероятность пробоя при напряжении на одну ступеньку выше этого напряжения (щ+Аи) равна V{uo+Au); однако первый пробой на этой ступени означает, что ранее пробоев не было. Для пробоя на первой ступени можно также записать

Pi = V(«o + A«)[l-V(«o)].

Аналогично для одного пробоя на второй ступени («о+2А«) следует, что при обеих пройденных ступенях не было пробоя и для пробоя на второй ступени имеет место

p, = V («о + 2А«) [1-V («о)] [ 1 - ("о + Аи)]. Для пробоя на fe-й ступени имеем

= V («о + /еА«) П [ 1 - V («о + /Д«)].

Величина функции суммарной частости в точке (uo+kAu) является суммой вероятностей пробоя на отдельных ступенях 2, причем число ступеней и абсолютный уровень напряжения определяется по величине ступени Аи и соотношению У («о-А") =0:

SAuo + kAu)=Zlv{u„ + iAu)l[[l-V{Uo + iAu)]}- (2.1)

При заданной функции поведения V{Unp) величина 5д„(«пр) отличается от нее тем больше, чем меньшей выбрана величина ступени Аи, т. е. чем больше ступеней необходимо для достижения определенного уровня напряжения. В этой связи рис. 2.7 показывает результаты вычислений с помощью ЭВМ: в качестве функции поведения выбрано нормированное нормальное

Естественно, желательно выбирать щ таким, чтобы пробой был маловероятен, т. е. чтобы V{uo)0.

2 Вероятности от ро до pk дают эмпирическую функцию плотности вероятности.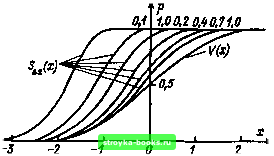

Рис. 2.7. Расчет функций суммарной частости прн различных уров-

нях ступени Ах функции поведения V(x), аппроксимированной распределением Л(0; 1): Ах = Aula; х = (и - ц)/а

распределение V{x)=N{0; 1) и в соответствии с формулой (2.1) при приведенной величине ступени Ах - Аи/а вычислена функция суммарной частости S(x). Видно, что функция суммарной частости располагается выше «достоверной» функции поведения и дает слишком большие значения вероятности пробоя. Для Дл:>1 (Дихт) разница между V{x) и S{x) незначительна.

Способ определения функции суммарной частости может быть также модифицирован, если на каждой ступени выполняют большое число опытов. Изучение взаимосвязи между функцией поведения и возможными функциями суммарной частости приводит к результату, аналогичному (2.1) [95]. Это означает, что такой способ можно использовать для определения малых квантилей пробивного напряжения [78, 96, 97] -см. п. 2.4.2.

2.1.3. Статистическое планирование эксперимента. Планирование большого количества высоковольтных измерений следует выполнять с учетом того, что стоимость испытаний, необходимого испытательного оборудования и затрат труда обслуживающего персонала, как правило, весьма значительна. При определении параметров эксперимента в первую очередь следует учитывать, что:

желательно сопоставление результатов с другими лабораторными исследованиями и известными практическими случаями;

определение обобщенной зависимости результатов обеспечивается целенаправленным изменением экспериментальных параметров и достаточно большим объемом выборки.

Чтобы достичь этого, предварительно необходимо точно определить статистическую цель экспериментов (например, оценка средней тенденции зависимости или всей функции рас-

пределения). При определении экспериментальных параметров следует использовать известные теоретические положения относительно исследуемых взаимосвязей (например, стримерную теорию газового разряда, накопление разрушений в твердом диэлектрике): Если имеет место большое число экспериментальных параметров и основные тенденции поведения неизвестны даже качественно, их обязательно следует определить с помощью заданного объема экспериментов. Для этого удобно использовать методы статистического планирования. В то время как при традиционном планировании эксперимента предполагается, что одна переменная изменяется ступенями, пока остальные остаются неизменными, при статистическом планировании все многочисленные переменные меняются одновременно. После относительно небольшого числа опытов удается отделить существенные переменные (главные факторы) от несущественных, а также осмыслить влияние изменения различных переменных (параметров). Метод статистического планирования впервые описал Р. А. Фишер [98]. В настоящее время в этой области существует весьма обширная математическая литература. Шефлеру принадлежит предназначенная Для инженеров работа, в которой опущены математические подробности, что характерно для работ Бокса [100], касающихся, однако, главным образом химии и металлургии. Предложенный Шефлером линейный метод прост для описания и поэтому должен быть использован для поясняющего примера. Это пояснение преследует лишь цель направлять читателя и облегчить ему переход к другой, специальной литературе (например, [157, 158]) и к более сложным примерам применительно к высоковольтной технике [159-161].

Рассмотрим случайный процесс, испытывающий влияние большого числа воздействий (переменных, параметров) Xi-Xh, причем направление и степень их влияния неизвестны. Для каждого параметра исследуются лишь два значения; их называют меньшей величиной (исходное состояние, обозначаемое как «-») и большей величиной (конечное состояние, обозначаемое как «-}-») этого параметра. При планировании эксперимента исходят из всех возможных комбинаций параметров. При k параметрах имеет место jV = 2 комбинаций, и поэтому необходимо также N отдельных опытов. В табл. 2.1 эти комбинации параметров изображены для случая k = 4 в так называемой матрице плана. Таблица может включать матрицы плана для fe = 2 (jV = = 4 опыта), k = 3 (jV = 8 опытов) и k = 4 (jV=16 опытов). В матрице ответов изображены результаты (ответы) уп, этих N опытов. При этом может оцениваться одна величина (например, Уи = «пр - напряжение пробоя), однако в матрицу ответа могут быть включены и несколько величин (например, У2] = Ш - начальное напряжение частичных разрядов; Ue - напряжецие