ЩОМЛа

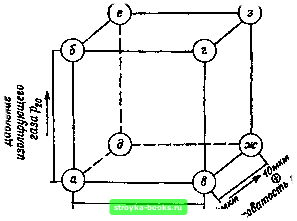ео,25мпа

Рис. 2.8. Схема статистического плана испытаний (к примеру 2.2)

Пример 2.2. Должны быть выбраны оптимальными параметры газового промежутка между коаксиальными цилиндрами в элегазе. (В практических случаях, естественно, одновременно можно выполнить теоретическую оптимизацию с помощью моделирования пробоя в элегазе [25].) Рассматривается давление газа р2 в диапазоне 0,25.. .0,40 МПа, радиус ri внутреннего электрода 3...6 см, радиус Г2 наружного электрода 15 см и наибольшая шероховатость р внутреннего электрода 4. ..10 мкм. Обозначая знаками «+» и «-» наибольшие н наименьшие значения воздействующих факторов в характеризующей их влияние матрице плана (табл. 2.2), можно получить

N=2 = 8 комбинаций, которые для ясности обозначены буквами /=а.....з.

Матрица независимых переменных получается при k=3 или Л=8 прямо из табл. 2.1. Целью оптимизации параметров является определение наиболее высокого напряжения пробоя промежутка, матрица ответов поэтому содержит только значения измеренных напряжений пробоя прн восьми комбинациях параметров (матрица ответов состоит из одного столбца, табл. 2.2). Для оценки построена матрица эффекта (2.2), содержащая в качестве сравниваемой величины среднее арифметическое «np = 1038 кВ [см. формулу (1.41)]. При наибольшей длине промежутка при t = l вызванное давлением элегаза «*npi = 469 кВ, причем радиус (t = 2) оказывает очевидное влияние (1г*др2=89 кВ). В завершение увеличение шероховатости (i=3) оказывает слабое отрицательное действие (и*прз=-14 кВ), что означает уменьшение пробивного напряжения. Связанное с изменением давления газа действие остается относительно сильным (t=12 или 13 сравнительно с t = 123). Можно заключить, что оптимальный диапазон лежит в области высоких давлений, больших радиусов внутреннего электрода и малой шероховатости (при !=ж). Это заключение должно быть наглядно и критически проверено.

При fe=3 серии экспериментов могут быть изображены в виде куба, вершины которого изображают экспериментальные точки (рис. 2.8). На-

Используемая запись означает не равенство i натуральному числу 123, а учет значений х\, Хг н х из матрицы плана. {Прим. перев.)

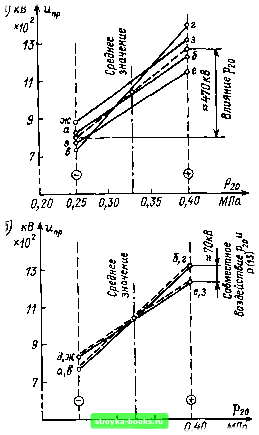0,20 0,25 0,30 0,35

Рис. 2.9. Графическое изображение влияния одиого параметра (рго) -о и влияние произведения двух параметров (р2о и р) - б (к примеру 2.2)

пример, нижняя грань куба соответствует исходному («-») давлению газа, верхняя - конечному («+»). Для радиуса используем левую и правую грани, для шероховатости переднюю и заднюю. Наиболее сильно различаются средние значения результатов, полученные в конечных состояниях (б, г, е, з) ив исходных состояниях (а, в, д, ж). Результатом двухфакторного взаимодействия является, например, для ( = 12 при конечном значении третьего фактора (шероховатости) половина разности между средними значениями результатов в точках е, з к д, ж или при начальном значении шероховатости - между б, г и а, в. Эти взаимосвязи могут быть изображены в форме любой нз диаграмм рис. 2.9. Наиболее отчетливо исследуемое влияние давления при принятой линейной зависимости величины пробивного напряжения получается при переходе от какого-либо исходного состояния (а, в, д, ж -рис. 2.9, а) к конечному состоянию (б, г, е, з) при усреднении имеющихся зависимостей. Результат взаимодействия (13) давления и шероховатости (рис. 2.9, б) получается из результата при конечном состо-