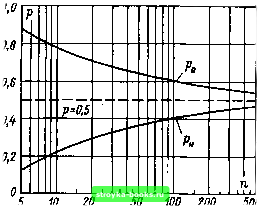Рис. 2.14. Доверительный интервал с границами р„ и р„ прн измеренной относительной частости Лп=0,5 в зависимости от объема выборки (при доверительной вероятности р=0,95)

ВИЮ l<fe<(n-1). Важно, однако, изучить также ступени, при которых р(«пр) близка к нулю или к единице.

Неизменность числа испытаний п на каждой ступени оказывает существенное влияние иа точность результатов. Если, например, на двух ступенях при весьма значительном числе испытаний вероятность пробоя оценивается практически точно, это жестко задает и, например, нормальную функцию распределения или какую-либо другую двухпараметрическую функцию распределения. Для определения п можно использовать доверительный интервал неизвестной вероятности (см. п. 1.3.1, рис. 1.11). Ширина доверительного интервала уменьшается с увеличением объема выборки. Рисунок 2.14 показывает, что для р = 0,50 можно задаться случайной ошибкой Ар=рв-0,5 = = 0,5-Рн (например, Ар = 0,1) и определить необходимое при этом число опытов п (объем выборки) (например, п=90).

Описанный путь, т. е. и интересующий нас квантиль пробивного напряжения, ограничены определенной вероятностью. При р=?0,5 аналогичная номограмма (см. рис. 2.14) легко получается из рис. 1.11 или рассчитывается с помощью выражений (1.58)--(1.60). Можно, однако, исходить и из всей функции распределения, обрабатывая ее соответствующим образом. Для математически точно заданной функции распределения объем выборки в опыте с нарастанием напряжения задается в п. 2.3.1. Основанный на методе доверительных интервалов способ для опытов с неизменным напряжением был модифицирован в работах [117, 118]. Здесь, как и в п. 2.3.1, используется его оригинальная публикация. Следует обязательно учитывать, что оп-

ределяемый объем выборки п должен быть приписан не общему числу отдельных опытов z, но числу воздействий на каждой из т ступеней.

Сказанное можно пояснить примером.

Пример 2.3. Необходимо определить функцию распределения для воздушной изоляции в автоматизированных опытах с помощью импульсов коммутационных напряжений. Статистические параметры опытов с неизменным напряжением должны быть заданы так, чтобы ошибка в определении вероятности пробоя не превышала Др<0,1. При рв = Ар+0,5 = 0,6 из рис. 2.14 получаем число опытов п*=90; выбираем п=100 опытов на ступень. В предварительных испытаниях было установлено, что при напряжении выше 1140 кВ встречаются лишь пробои, а ниже 1065 кВ - только непробои. Это определяет интересующий нас диапазон напряжения Д«в = 75 кВ. Поскольку импульсный генератор позволяет получать лишь дискретные значения напряжения ступени Д«р=5 кВ, то возможное число ступеней получаем по формуле (2.4)-тт = 15. Ввиду относительно большого числа опытов на каждой ступени в качестве подходящего рассматривается число ступеней т=12, что позволяет определить различие напряжения каждой ступени по выражению (2.5)-Д«»6 кВ. Общее число отдельных опытов по формуле (2.3) составляет z=1200. Напряжение первой ступени лежит на уровне 1065 кВ (если при п=100 приложениях напряжения не будет ни одного пробоя, эта ступень не будет учитываться). Поскольку изолирующие свойства воздушной изоляции восстанавливаются относительно быстро, необходимое генератору время между двумя импульсами Д<=30 с достаточно велико.

В приведенном примере описаны относительно точные измерения, при грубых оценках исходят из существенно меньшего числа опытов, а прецизионные измерения, напротив, требуют значительно больших затрат. Если функция распределения должна быть определена вплоть до весьма малых квантилей, необходимо принять очень большое число опытов на каждой ступени (например, в диапазоне р(ыпр)<0,03 или р(мпр)>0,97 должно быть предусмотрено п>400) [78, 96, 119]. Столь большое число измерений требует длительного времени, поэтому следует обратить особое внимание на постоянство параметров эксперимента и снижение эффекта тренировки (в особенности из-за обгорания электродов и образования поверхностных слоев на электродах -см., например, [25]) [78, 96, 119, 120, 121].

2.2.2. Гарантирование независимости опытов. Если для каждого нового опыта не используется новое исследуемое устройство, то следует контролировать взаимную независимость реализаций. Причиной зависимости результата данного опыта от результата предыдущего являются физические изменения объекта исследования, обусловленные взаимосвязью между собственно испытуемым устройством (изолирующим материалом, электродами), видом напряжения, вкладом энергии при предшествовавших частичных разрядах или пробоях, а также выбранной длительностью паузы между опытами.

При использовании атмосферного воздуха в качестве изоляции практически неограниченный объем газа приводит к его постоянному объему, так что при длительности паузы при-

мерно в несколько секунд воздействия предшествующей элек--трической дуги уже не заметно. Основные изменения в электродах происходят под действием частичных разрядов или пробоев. Электроды с малым радиусом кривизны (острия) особенно чувствительны к обгоранию, а электроды с малой площадью поверхности - к увеличению шероховатости поверхности и образованию неметаллического слоя. Если необходимо исследовать склонный к этому промежуток, то, с одной стороны, следует предварительно принять соответствующие меры в отношении техники эксперимента, чтобы противодействовать его изменениям (например, ограничить с помощью предвключен-ного сопротивления или параллельно включенного разрядника выделяющуюся при пробое энергию), а с другой - контролировать независимость реализаций в процессе эксперимента (см. п. 2.3.2).

При изоляции сжатым газом к упомянутым для воздушной изоляции проблемам, связанным с электродами, добавляются изменения в ограниченном объеме газа. С одной стороны, следует учитывать, что разряды приводят к химическим реакциям [25] и поэтому к изменению состава газа, с другой - иметь в виду, что остающийся после пробоя пространственный заряд рекомбинирует относительно медленно. Если после пробоя последующее нагружение происходит до рекомбинации пространственного заряда, то образуется измененное распределение напряженности электрического поля, которое ускоряет или затрудняет развитие разряда по сравнению со случаем отсутствия объемного заряда. Если в изоляцию привнесена поверхность твердого диэлектрика, например, поддерживающего изолятор, то, как и при использовании атмосферного воздуха в качестве изоляции, на поверхности образуются связанные заряды [50, 51], приводящие к изменениям результатов эксперимента. При этом следует чрезвычайно осторожно выбирать длительность паузы между опытами [25] и стремиться активно ее использовать [86]. Для этого в паузе между двумя - чаще всего импульсными - нагружениями изоляции прикладывают ограниченное по амплитуде переменное напряжение (примерно 10--20% импульсного напряжения), ускоряющее рекомбинацию пространственных и объемных зарядов. Контроль независимости реализаций в процессе измерений остается необходимым.

При использовании жидкой изоляции имеют место те же соотношения, что и при изоляции сжатым газом, лишь химические изменения под действием разрядов (разложение, газообразование) более интенсивны и подвижность пространственного заряда меньше. Опыты с неизменным напряжением могут выполняться лишь в особых случаях при достаточной длительности паузы; следует переходить к опытам с нарастающим на-