1,0 0,8 0,6 0,it

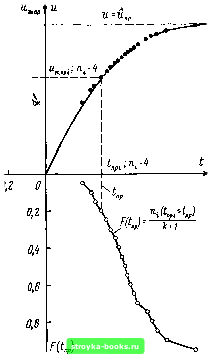Рис. 2.16. Определение функций поведения мгновенных значений напряжения пробоя f («т пр) и времени до пробоя F(tnv) в опытах с неизменным напряжением при импульсах коммутационных перенапряжений « и 19 пробоях в серии из п=25 опытов Светлые точки - суммарная частость пробоя промежутка f (« др* " пр* темные точки - мгновенное значение напряжения пробоя „р! крестики - оценка функции поведения V*; р - вероятность пробоя в опытах с неизменным напряжением; мгновенное значение напряжения пробоя; РМщ пр* пp ~~ суммарная частость; V*(u оценка функции поведения; („р - время до пробоя

на максимуме и на спаде импульса в качестве мгновенного должно быть принято общее значение максимального напряжения Ыпр.

В соответствии с работами [126-129] можно использовать также и общее число испытаний п, причем в опытах с неизменным напряжением на основе вероятностей пробоя получают окончательно функцию V*(«mnp; Ипр), тесно связанную с функцией поведения V(«np) (рис. 2.16). Если влияние формы импульса, т. е. длительности нарастания напряжения, на напряжение пробоя при коммутационных импульсах отсутствует, эти функции могут быть пересчитаны одна по другой [126, 129 -

Рис. 2.17. Определение контурных ли- MB НИИ [129]

Опыты с иеизмеииым напряжением для восьми различных уровней импульсов коммутационных перенапряжений с формой волны

680/5200; опорный изолятор в воздухе /

У%„;}=0,991

Контурная линия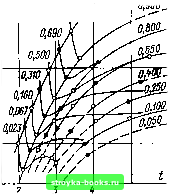

130]. Как правило, однако, этого не делают. Функция V*(«mnp; Ыпр) может оказать помощь при выполнении координации изоляции и изучении чрезвычайно сложных вспомогательных соотношений статистики при сопоставлении воздушных изолирующих устройств: для используемого напряжения строится кривая напряжение- время и мгновенные значения, приводящие к одинаковым вероятностям пробоя соединяются так называемой контурной линией (рис. 2.17). Повторяя эти действия при различных формах импульса, получают семейство контурных линий (рис. 2.18). Их огибающая при требуемой вероятности называется «минимальной контурной линией» [на рис. 2.18 штрихами они нанесены при pmin = = 0,50 (кривая /) и при Pmin=0,023 (кривая 2)]. Минимальные контурные линии (рис. 2.19) являются чрезвычайно полезным средством, позволяющим обсуждать поведение воздушной изоляции в расширенном возможном диапазоне коммутационных импульсов. Естественно, что контурные линии можно получать также, изучая функции поведения при различных формах

хЮ тс

680/5200 тотоомкс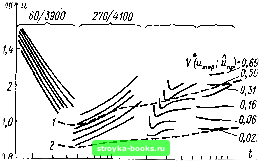

0,2 0,5 1,0

5,0 х10 мкс

Рис. 2.18. Контурные линии для четырех уровней импульсов коммутационных перенапряжений и определение минимальной контурной линии [129] Опорный изолятор в воздухе; Рщ- вероятность минимальной контурной линии

импульсов и представляя затем в форме рис. 2.19. Предложенный в работе [129] способ при сложных измерениях (не только максимального напряжения, но и мгновенного значения) обладает преимуществом малых затрат. Для получения всевозможных многочисленных сведений, представляющих интерес как для понимания физики явлений, так и в технических приложениях, опыты с неизменным напряжением (и не только в подобной воздушной изоляции) должны быть также тщательно запланированы.

2.2.4. Аппроксимация функции поведения теоретическими функциями распределения. Если функция поведения меняется монотонно (см. рис. 2.15), то нет никаких сомнений, что она может быть аппроксимирована какой-либо теоретической функцией распределения. При этом необходимо учитывать, что для этого вовсе не требуется воспроизводить теоретико-вероятностную природу явлений, а можно использовать лишь хорошо разработанный прием математической формализации на основе теоретической функции распределения. По сути взаимосвязь между вероятностью пробоя и напряжением (или другой задаваемой величиной) остается функцией поведения, как это отмечалось при оценках параметров изоляции (см. п. 1.1.1).

Для аппроксимации функции поведения известными функциями распределения должны учитываться следующие основные моменты.

Функция распределения должна достаточно хорошо совпадать с функцией поведения. Критерий качества аппроксимации может быть получен, с одной стороны, на основании физической или технической постановки задачи, а с другой - при использовании статистических испытаний распределений (см. п. 1.5.1).

Теоретическая функция распределения (см. § 1.3) должна быть в состоянии по сути связать с исследуемым физическим процессом соответствующую модель. Подобная взаимосвязь существует, например, между процессом зажигания газового разряда и моделью на основе экстремального распределения

[25, 130, 131]. Развиваю-

МВ 1Л

щийся из частичных разрядов пробой в воздухе удобно описывать нормальным распределе-

1000 мкс

Рис. 2.19. Избранные квантили напряжения пробоя в зависимости от длительности фронта, определенные по методу минимальной контурной линии [129] (опорный изолятор в воздухе)