нием. Другие указания об этом сделаны в описаниях теоретических функций распределения в п. 1.3.2 и в гл. 4 при описании возможностей изоляции.

Наконец, используемая для аппроксимации функции поведения теоретическая функция распределения должна быть также удобна для инженерных расчетов. Следует избегать сложных аппроксимаций.

Взаимосвязь между приведенной в табл. 2.4 эмпирической функцией поведения и теоретической функцией распределения устанавливается главным образом с помощью изображения на вероятностной сетке, а еще лучше с помощью линейной регрессии (см. п. 1.4.3). В примере 1.29 уже обсуждалась аппроксимация нормальным распределением. К этой оценке в данном случае ничего добавлять не нужно. Имеющиеся для нормального распределения обширные статистические разработки (п. 1.3.2) делают возможными грубые оценки доверительных интервалов и доверительных границ. В качестве объема выборки при этом следует принять число воздействий п на одной ступени напряжения. Для вероятностей пробоя, как и для любого квантиля приближающего функции поведения нормального распределения, доверительные границы остаются равными вычисленным [38, 116, 132, 133]. Оценка опытов с неизменным напряжением может быть выполнена по методу, предложенному в работе [37], и без регрессионных расчетов, однако расчеты регрессии при использовании микро-ЭВМ чрезвычайно просты и более предпочтительны

Для аппроксимации эмпирических функций поведения непрерывных случайных величин вместе с нормальным распределением можно использовать и другие функции распределения. Предпочтительными являются экстремальные функции распределения. Действия в этом случае должны быть пояснены аппроксимацией с помощью двойного экспоненциального распределения.

Пример 2.6. Изображенная на рис. 2.15 и заданная табл. 2.4 эмпирическая функция поведения должна быть исследована путем приближения с помощью двойного экспоненциального распределения. Для этого прежде всего была выполнена точечная и доверительная оценка на вероятностной сетке двойного экспоненциального распределения (рис. 2.20). Установлено, что через все доверительные интервалы можно провести прямую линию. Наилучшая прямая, однако, должна быть найдена путем регрессионного анализа. Для этого ордината линеаризуется с помощью преобразования, обратного для двойной экспоненты:

«/=ln[-ln(l-p)], (2.6)

Доверительные границы всей прямой регрессии [18, 83] являются доверительными границами для любого квантиля функции поведения.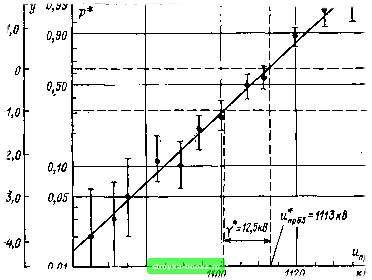

1080

Рис. 2.20. Аппроксимация эмпирической функции р* поведения изолирующего промежутка со слабонеоднородиым полем в воздухе с помощью двойного экспоненциального распределения (к примеру 2.6)

и в табл. 2.5 рассматривается лищь линейная задача. С преобразованной вероятностью пробоя у и пробивным напряжением «пр=х связана прямая регрессии

у = аухЛ- ЬухХ = - 88,7 + 0,0797х,

откуда могут быть вычислены параметры двойного экспоненциального распределения:

«np63=-W (2-)

V* = Ibyx, (2.8)

которые можно сравнить с нормальным распределением из примера 1.29, уравнения (1.128) и (1.129). В данном случае и*прва=1113 кВ и у*=\2,Ь кВ. Описываемое этими параметрами двойное экспоненциальное распределение на рис. 2.20 проходит через все доверительные интервалы вероятности пробоя и хорошо аппроксимирует эмпирическую функцию поведения. Для подтверждения этого может быть, например, выполнен тест Колмогорова (см. п. 1.5.1).

2.2.5. Схема оценки и расчета. На рис. 2.21 еще раз представлены все отдельные шаги выполнения опытов с неизменным напряжением. После подготовки и выполнения эксперимента выполняется оценка протокола экспериментов на всех т ступенях напряжения. Они должны быть проверены на взаимную независимость опытов и после установления независимости оцениваться далее. После определения вероятностей пробоя на каждой ступени напряжения образуется эмпирическая

х= 1098 кВ; Sx = 22,8 кВ;

4 = 521,8 кВ»

у = -1,188; Sy = 1,839;

si = 3,381

Коэффициент ковариации Sxy = 41,6; коэффициент корреляции г = 0,992; коэффициенты регрессии: Ьух = 0,0797, Оух =

= -88,7, прямая регрессии у = -88,7 + 0,0797 х

функция поведения, которая при монотонно нарастающем характере может быть аппроксимирована какой-либо теоретической функцией распределения. После контроля и аппроксимации могут быть получены параметры функции поведения и квантили, важные в технических приложениях. Результаты эксперимента должны быть представлены в форме, удобной для их дальнейшей интерпретации. Для каждого из описанных шагов в предлагаемой книге указан способ математической формализации; цифры в скобках на рис. 2.21 обозначают соответствующий раздел.

Поскольку оценка каждого варианта состоит из известных математических и логических шагов, ее выполнение с помощью ЭВМ не составляет труда, тем более что протокол эксперимента в современных испытательных установках может быть введен в расчет немедленно [104, 105]. Во многих высоковольтных лабораториях существуют программы расчета для статистической оценки в процессе получения результатов [41,103, 134, 135]. Программы для отдельных операций приводятся в опубликованной книге [136] и в крупных вычислительных центрах. Передача программ не составляет также принципиальных затруднений, скорее наоборот, так как каждая из имеющихся