
 |
|
Главная Среднее значение величин [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 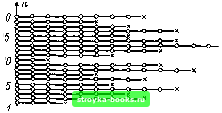 0,95 0,30 0,70 0,60 0,50 0,W 0,30 0,20 0,10
110 110 130 по 150 160 170 180 130 200 кВ Рис. 2.33. Определение функции поведения по функции суммарной частости, описываемой нормальным распределением (пример 2.11) Импульсы коммутационных перенапряжений +50/5000 чем меньше величина ступени, тем меньше должно быть выбрано начальное напряжение. Пример 2.11. Необходимо определить функцию поведения промежутка острне - плоскость в масле (расстояние между электродами d=50 мм). Прямое эмпирическое исследование нецелесообразно [94, 124], поскольку ход функции суммарной частости уже известен. До начала эксперимента необходимо оценить среднее значение функции суммарной частости «пр 50S = 1д» = ISOIkB и стандартное отклонение 0д„ = 0.08р,д„ = 12 кВ. Выбираем величину ступени Дц=5 кВ. Для оценочной величины Д«/<Тд„ отсюда следует значение чуть более 0,4, для которого рис. 2.31 дает Дх»0,25. Нормированная верхняя граница начального напряжения задается как хов=-2,7 (рис. 2.32), так что = (Хд+л:ов<1„ = 150-2,7-12 « «118 кВ. При выборе начального напряжения «о=П0 кВ<Мов функция 5д„ (мр) будет определена точно. Несмотря на то, что «о должно изменяться, здесь для наглядности оно поддерживается постоянным. Число опытов фиксировано: /г=20. Результаты экспериментов наглядно представлены на рнс. 2.33. Параметры функции суммарной частости оцениваются как = мр = = 148 кВ и Одц = = 15 кВ. С помощью эквивалентного соотношения Ли/5дц = 0,33 (рис. 2.30, а) следует, что а\х = 0,65 и цд. = - 0,88 (рис. 2.30, б). Используя выражения (2.19) и (2.20), вычисляем параметры функции распределения (нормальное распределение) s=23 кВ и «np5ov = 169 кВ, изображенного на рис. 2.33. Если бы этот расчет не был выполнен, то в качестве математического ожидания было бы принято лежащее ниже напряжение Мпр 608=148 кВ. Процесс пересчета можно вполне успешно контролировать по результатам эксперимента [124]. Пусть (рис. 2.34), как в предыдущем примере, по функции суммарной частости 5ди(«пр) определяется функция поведения V (Ипр) воздушного промежутка (для наглядности измеренные значения опущены). Прямое определение функции поведения в опытах с неизменным напряжением дает доверительные интервалы, которые очень хорошо подходят к функции поведения, пересчитанной с 5ди(«пр). Этот метод очень удобен для использования и, поскольку в опытах с неизменным напряжением также нет взаимной зависимости, приспособлен для контроля. При аналогичном контроле масляного промежутка [124] подобное совпадение имеет место, только если в опытах с неизменным напряжением используется длительность паузы более А<п = 300 с (рис. 2.35). При более коротких паузах (Ап = 30 с) в опытах с неизменным напряжением имеет место взаимное влияние, искажающее результаты. Причиной этого является наличие пространственного заряда и после пробоя, не имеющего возможности рекомбинировать при более коротких паузах (124, 137, 138]. Для жидкой изоляции и герметизированных устройств [25] рекомендуется определять функцию поведения через функцию суммарной частости. Если функция поведения определяется вплоть до весьма малых вероятностей, рекомендуется выполнять опыты с неизменным напряжением при большем числе нагружений на каждой ступени (т>1) [97, 139, 140]. Начиная с некоторого напряжения Ыо lero увеличивают ступенями по Аы, пока на какой-либо ступени не наступает пробой. При этом неважно, на котором из т приложений напряжения на данной ступени не возникает. После пробоя опыт прекращается независимо от того, сколько еще воздействий на данной ступени следовало бы сделать, и для дальнейших экспериментов напряжение вновь снижается до «о. Вероятность того, что на данной сту- 0,99 0,95 0,90 0,80 0,70 0,50 0,30 0,10 0,05 0,01
55 Ш /с5 Рис. 2.34. Функция суммарной частости и функция поведения искрового промежутка острие - плоскость в воздухе d=»150 мм; импульсы атмосферных перенапряжений 1,2/50 0,99 0,95 0,90 0,80 0,70 0,50 0,30 0,10 0,05 0,01
200 230 2SQ 290 кВ Рис. 2.35. Функция суммарной частости и функция поведения изолирующего промежутка острие - плоскость в масле d=70 мм; импульсы коммутационных перенапряжений 200/3000 пени при т приложениях напряжения не будет пробоя, задается выражением PNkn-V{Uo+kAu)r. (2.23) С вероятностью pDk=l-pNk=l-[l-V{uo + kAu)r (2.24) имеет место по меньшей мере один пробой, причем после первого пробоя испытания прекращаются (95, 96]. Эти соотношения позволяют рассчитывать функцию суммарной частости по функции поведения (см. п. 2.1.2) только при т повторных воздействиях (т>1). Для значения функции суммарной частости в точке «о при известной функции поведения V (Uo + kAu) имеем Sa {uo + kAu) = = Е (l-ll-l/(«„-f 1Аы)]»)П[1-У(«о + /А«)]4. (2.25) 1=1 I 1-\ ] При т=1 уравнение (2.25) переходит в (2.1). Наоборот, при известной функции суммарной частости 5ди(«пр), определенной при т>1 приложениях напряжения на каждой ступени, аналогичным образом из уравнения (2,10) может быть вычислена функция поведения V(«Hp)=l-/ S (Мпр) - S («пр - Д") 1 - S (м (2.26) 165 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 0.0022 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||