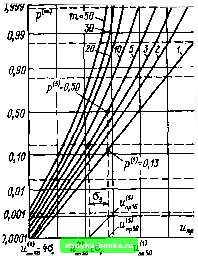Рис. 2.43. Вероятность пробоя р*"*), при котврой при числе воздействий m на каждой ступени напряжением «пр происходит по меньшей мере один пробой [146] (pi<"-iV(«">np6o; ffi*), считается известной; любому напряжению Мпр соответствует своя вероятность р"(«ир) и соответственно р>(Ипр)-в m приложениях напряжения)

поведения при /п = 5 нагруже-ниях на ступень соответствует на рис. 2.43 значение рС) = 0,13 при т= 1. Равным образом определение 50 %-ного квантиля при /п = 5 приводит к 13 %-ному квантилю при т=1. Эта взаимосвязь представлена еще раз для различных т на рис. 2.44, на котором изображена зависимость вероятности пробоя р<> при т=\, соответствующая 50 %-ному напряжению пробоя ufnpso в зависимости от т. На практике по рис. 2.44 можно также вначале определить соответствующее желаемому квантилю (например, «"пр1о> т. е. р<)=0,1) требуемое число приложений напряжения на ступень т (например, т=7). Пусть выполнена процедура расширенного метода «вверх - вниз» (как на рис. 2.42 при т = 7) и как для т=1 определен эмпирический квантиль «"*пр5о. Полученная величина напряжения является также оценкой для искомого квантиля ы*пр1о- Если, кроме того, известным методом определено ы<*пр5о при т=1, то имеются уже два эмпирических квантиля нормального распределения (и*пр5о; oi), с помощью которых может быть просто определена и СГь

Таким образом, расширенный метод «вверх-вниз» дает лучшую оценку дисперсии, чем классический способ.

Разумеется, необходимо учитывать, что при т>1 большинство функций поведения не обладает нормальным распределением (рис. 2.43). Метод «вверх - вниз», однако, предложен для нормально распределенных генеральных совокупностей. Поэтому функции поведения У"(Ыпр) должны быть аппроксимированы нормальными распределениями (Unpso ; сгт), причем зависящая от т связь между От и ai изображена на рис. 2.45. Поскольку принятие нормального распределения для F""M"np) является лишь приближенным, достаточно вычислить «прбо как среднее арифметическое и обойтись без трудоемких расчетов по формулам (2.27) и (2.32).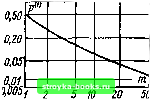

1 2 5 10 20 50

Рис. 2.44. Вероятность пробоя рС) при напряжении «"пр 50 в зависимости от числа воздействий m [146] (в m воздействиях с вероятностью р™ происходит по меньшей мере один пробой)

Рис. 2.45. Отношение стандартных отклонений при m и при одном приложении напряжения на ступень при нормальном распределении [146]

В работах [145, 146] описаны исследования, основанные на расширенном методе «вверх - вниз» и имеющие большое значение для выбора параметров эксперимента. Если считать точ-

ность оценки равной стандартному отклонению Оа среднего значения и (полученного по стандартному отклонению От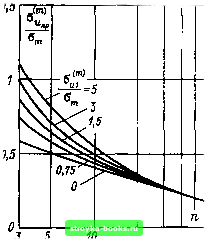

20 30 40 60

Рис. 2.46. Качество оценки математического ожидания «("Чпр 50, определяемое по его относительному стандартному отклонению в зависимости от числа я выполняемых серий [146] (a<"ui/crm - относительный разброс напряжения первого пробоя; Аи=От - величина ступени)

40 30

20 10

3 5

20 30 4060

Рис. 2.47. Усредненное число необходимых серий п в зависимости от числа выполняемых серий п [146] (a<">ui/crm - относительный разброс напряжения первого пробоя; Д« = ат - величина ступени)

Рис. 2.48. Максимальное общее число серий rtmax в зависимости от числа выполняемых серий п [146] (a")ui/am - относительный разброс напряжения первого пробоя; kusa - величина ступени)

50 W

30 20

10 :

20 30 4050

нормального распределения при аппроксимации У"» ("пр)), то точность возрастает с числом выполненных серий п (рис. 2.46). Разумеется, стандартное отклонение аих первого пробоя (ср. с рис. 2.38) влияет на точность оценки при малом

числе выполняемых серий п. При /г>30 величина aui не оказывает никакого влияния.

Метод «вверх - вниз» дает п первых пробоев (рис. 2.37); при расширенном методе в соответствии с рис. 2.42 оно равно числу требуемых серий п. Поскольку этот первый пробой обладает случайным разбросом., число реализуемых серий п зависит от его стандартного отклонения аЙ- Число выполняемых серий может быть больше или меньше требуемого числа и существенноависит от числа серий п (рис. 2.47). При /г>20 значения п и п практически одинаковы, при меньших п рассматривается еще и зависимость его от OuT-

Затраты, ограничивающие применение расширенного метода «вверх-вниз», определяются максимальным общим числом серий rtmax, которое растет, естественно, быстрее, чем число выполняемых серий (рис. 2.48). Оценка требуемых затрат приведена на рис. 2.47 и 2.48.

В среднем общее число приложений напряжения

Nwnm (2.34)

определяет погрешность оценок. Путем моделирования [146] были определены стандартные отклонения Oi-аУ стандартного отклонения (Т, и оценки квантили Ыпрд-(Тм"* (рис. 2.49). С их помощью можно оценить доверительные границы, как это описано в примере 2.12 [146].

Пример 2.13. С помощью расширенного метода «вверх - вниз» необходимо оценить 50%-ное и 2 %-ное напряжение пробоя, а также стандартное отклоиение изолирующего промежутка.

Прежде всего определяется «*пр so при числе приложений напряжения на ступени т=1. Чтобы исключить влияние разброса первого пробоя, в соответствии с рис. 2.46 выбирается я=30. Начальное напряжение «о весьма слабо влияет на результаты; на основании предварительных оценок исследуемого промежутка при «о =1000 кВ не должно возникнуть ни одного пробоя. Равным образом на основании более ранних исследований известно, что