aJO.O 0,4 0,2

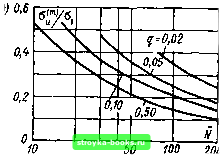30 50 100 200 300 400

Рис. 2.49. Оценка погрешности метода «вверх--вниз» [146]: а - стандартное отклонение a*j*оценки 0\\ б - стандартное отклонение аи оценки «("Чир « ~""пр50 "Р" «-25; m=l и «пр ц при т=6 (ге произвольно); 2 - прн re=i25;

т=\ н ИпрО.Об"?" " произвольно): 3 - прн «=25; т=1 и «„р д "Р

ш=34 (« произвольно); - "пр 60произвольно; ш = 1); 5 - u„ н "про,ов "Р" т-11 (ге произвольно); 9 -порядок квантиля

коэффициент вариации имеет величину порядка 0,06. Поскольку величина ступени А« должна быть установлена близкой к Oi, ее принимают приближенно А««0,06 «0=60 кВ. Выполнение эксперимента показано в табл. 2.7, п. 1. Простая оценка среднего значения дает «*пр5о=1194 кВ. Рисунок 2.46

дает для л=30 стандартное отклонение среднего значения а/ =0,25(Т1.Од-

"Р

новременно с его верхней оценкой si =0,06 1194=72 кВ определяем s,} =

"пр

=0,25si=18 кВ. Диапазон [«пр50* ] = [1158 кВ: 1230 кВ] можно

считать 95 %-ным доверительным диапазоном для «пр so.

Перейдем к определению «*пр 0,02. Рисунок 2.44 дает для /><i)=0,02 необходимое число приложений напряжения иа ступень т=34. Величина ступени должна быть принята А«»аз4. Рисунок 2.45 дает аз4~0,5 а1«36кВ, и поэтому А«=36 кВ. Общее число опытов должно лежать между 100 и 200. При N=mn и т=34 будет выбрано я=5. Если будет принято ан1 =

= ffj, (разброс первого пробоя равен разбросу среднего значения), то "Р ,,,

получаема„, = о, = 0,25а « 18 кВ и aui/as4=0,5. Из рис. 2.47 далее сле-

"Р

дует для я=5 среднее число требуемых серий я=4 и из рис. 2.48 максимальное число серий rtmai = 6. В качестве начального напряжения предусмотрено принять 2 %-ное пробивное напряжение, для чего можно обойтись несколькими сериями. Это дает

"о « "пр 0.02 = «пр 50 - 2.05О, = 1047 кВ.

Теперь все параметры эксперимента установлены и можно выполнять процедуру метода «вверх - вниз» при т=34 (результаты приведены в табл. 2.7, п. 2). Определяя среднее значение, находим «„рМ =1083 кВ = = «пр*о,о2 где а, может быть вычислено как разность двух квантилей:

3 "пр50-"пр0.02

2,05

Напряжение Uf, к В

о •о

Число пробоев на ступени

с помощью рис. 2.49, а и соответствующего используемым параметрам эксперимента («пр so при л=30, т=1 и «пр 0,02 при п=5, т=34) среднего суммарного числа опытов

iV = (H -0,25 (п-1)) т= 102

осталось оценить стандартное отклонение а*„ стандартного отклонения а: s.() = 0,25 si=13,5 кВ. Диапазон [Si±2s,()]=[54 кВ±27 кВ]=[27 кВ; 81 кВ] является доверительным диапазоном для исследуемого стандартного отклонения. Остается определить разброс аи"> 2 %-ного пробивного напряжения

(=0,02) по рис. 2.49, б при ЛГ=102 как (т„(")=0.35 si=19 кВ: 95 %-иый

доверительный интервал 2 %-иого пробивного напряжения составляет

1«пр50 ± 2«Г] = [«{,о,02 ± 2sl?*] = [1083 кВ±38 кВ]=[1045 кВ; 1121 кВ].

В заключение вычисляется верхний доверительный интервал для «пр so при точном значении Sj=54 кВ. Из рис. 2.46 следует для я=30, что а" /а, = 0,25; s = 0,25s, = 13,5 кВ; 95 %-ным доверительным нитерва-

пр пр

лом 50 %-ного пробивного напряжения при этом является

= [1194 кВ ± 27 кВ] = [1167 кВ; 1221 кВ].

Результаты доверительных оценок для 50 %-ного напряжения пробоя: «gi= (1194+27) кВ; 2 %-ного напряжения пробоя: «<fj;J o2= (1083±38) кВ; стандартного отклонения: О)»"">= (54±27) кВ.

«пр50±

2.4.2. Методы определения квантилей малого порядка. Как

уже отмечалось в п. 2.3.4, «малые» квантили пробивного напряжения могут быть определены в опытах с нарастающим напряжением при т приложениях напряжения на ступень напряжения. Если сразу же после первого пробоя опыт прерывается (рис. 2.50), то при п повторениях будет получена эмпирическая функция суммарной частости соответствующего напряжения пробоя Unpq, при т нагружениях которым образуется по меньшей мере один пробой. Если п достаточно велико и начальное напряжение варьируется точно (см. п. 2.3.1), то, например, мате-

-L-f!

<

Рнс. 2.50. Определение малых квантилей напряжения пробоя в опытах с нарастающим напряжением (т>1)

п - число серий; а - номер ступени