магическое ожидание E(Unpq) =u„pq будет именно квантилем малого чюрядка.

Многочисленными авторами (в том числе [137, 147, 148]) исследовалась методика, дающая при возможно меньшем числе пробоев и допустимом общем числе приложений напряжения информацию относительно квантилей <7<0,1, а также определяющая статистически выдерживаемое напряжение. Аналогичные методы имеются для «больших» квантилей q>0,9 и для статистического напряжения пробоя разрядника или искрового промежутка.

В простейшем случае такие опыты с нарастающим напряжением выполняются лишь однажды с начального напряжения

Uo = «пр 50 - (2-35)

при т>1 (число п=1 должно быть использовано для Ыпрво и s; k>0). Под статистически выдерживаемым напряжением понимают такой наибольший уровень напряжения

"пр5 = "пр5о-ps. (2-36)

при котором при всех т нагружениях не возникает ни одного пробоя. Число ступеней, при которых происходит первый пробой, является случайной величиной А. Для случайной величины выдерживаемого напряжения при этом имеем

{/пр, = «о + (-1)Аы, (2.37)

а для его математического ожидания

£(пр,) = Ыо-А« + А«£() = "пр,. (2.38)

Вероятность того, что первый пробой произойдет на ступени а, вычисляют аналогично рассмотренным ранее [см. выражения (2.1) -(2.25)] как

Р (Л = с) = [1 -(1 -У (а))-»] П (1 -V {1)Г, (2.39)

где V(a) или V(i)-уровни соответствующих пробивных напряжений (значения функции поведения). При математическом ожидании

Е {А) tailed (а))-] Д (1 -V (О)" (2.40)

а<=1 1=0

и С учетом формулы (2.38) для математического ожидания статистически выдерживаемого напряжения получаем

E{U„p,)==Ыпр, = "пр bo-s{k + --

£ а [1 -(1 -К (а))-] П (1 -V {i)A = «прво-ps, (2.41)

а=1 1=0 )

0,50 0,40 0,30

0,20 0,10

0,05 0,025 0,010

0,005 0,003

-JO 0,5 1,0 1,5 2,0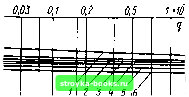

. 2,5

Рис. 2.51. Зависимость ожидаемого квантиля Unp , и среднего квадратического отклонения sp от начального напряжения Ыо (число опытов иа ступени т;

величина ступени Au/s) Среднее квадратическое отклонение Sp множителя р при Ди/s. равном 0,1, н ш, равном 20. 10, 5 (кривые 1-3), и Ды/s, равном 0.5, и т, равнсм 20, 10, 5 (кривые i-6); множитель р (2.36) и порядок q квантиля «пр? Ч" Д"/* равном 0,5, и т, равном 5, 10, 20 (кривые 4-6), и Ди/s, равном 0,1, и ш. равном 5, 10, 20 (кривые 1-3); (7 - порядок квантиля - начального напряжения "пр,,""»; ft - множитель для определения начального напряжения (2.35)

4,0 3,8 3,6 3,4 3,2 3,0

зависящее от начального значения «о (определяемого в соответствии с (2.35) по величине k), числа приложений напряжения на ступени т и величины ступеньки Ды. Для дисперсии числа ступеней, при котором происходит первый пробой, имеем

Д(Л) = £(Л)-[£(Л)р, и таким образом для дисперсии выдерживаемого напряжения

DMf/np ,) = {Auf f Z I -(1 - V (с))-] П (1 - V (0)" -

fl-1

£а[1-(1-У(а))"]П (1-(0)"

Lfl=l i=0

(2.42)

Дисперсия выдерживаемого напряжения может быть выражена через дисперсию Sp с помощью множителя р уравнением (2.36).

В предположении, что V(Uap), а потому и V(a), удовлетворяют нормальному распределению, выполнены исследования влияния на результаты эксперимента начального напряжения «о (полученного в соответствии с k, рис. 2.51), числа нагружений напряжения т (рис. 2.52) и величины ступени Ди (рис. 2.53) [149]. Если начальное напряжение выбрано Uo<w„p5o-3s, то оно не влияет ни на математическое ожидание, ни на дисперсию статистически выдерживаемого напряжения. Число воздействий на одной ступени т существенно влияет на математическое ожидание и слабо - на дисперсию. Чем больше т, тем меньше

Рис. 2.52. Зависимость ожидаемого квайтиля «пр q я среднего квадратического отклонения sp от числа опытов иа ступени т (начальное напряжение Uo="np50-3s = Unp 0,013".

величина ступени Дм/s)

Среднее квадратическое отклонение sp множителя Р при Ди/s, равном 0.10; 0,25; 0,50 - соответственно кривые 1-3; множитель Р (2.36) и порядок q квантиля «пр? при Au/s, равном 0,50; 0,25; 0,10,- соответственно кривые З-l

порядок ожидаемого

квантиля (рис. 2.52). 0,025-Хотя малые величины

ступени и приводят к ма- gg-fg.

лым квантилям, их влия-

ние на дисперсию умень- ">"°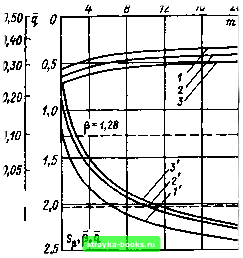

шается с величиной ступени (рис. 2.53). Эти взаимосвязи необходимо пояснить примером.

0,50 0,40 0,30

0,20

0,10

0,05 0J025

0,010

0,005 0,003

- О

0,5 1,0 1,5 2,0 2,5

0,1 0,1 0,3 0,4 0,5

Рис. 2.53. Зависимость квантиля «пр в и среднего квадратического отклонения S от величины ступени Au/s Среднее квадратическое отклонение sp множителя р при т, равном 20, 10, 5, - кривые 1-3; множитель р (2.36) и порядок q квантиля aj,p при т, равном 5, 10, 2, -

кривые З-l