оооооскхюо,

и, 10/10 10/10. 10/10 6)

" 5/10 * 9/10\ 10/10 2/10}. 7/10 \ 10/10\ 6/10\ 9/10

о ьооо ооо о

0/iO\ 4/10} 7J10

0/10 \

1/10 \

0/10 \ 0/1 о \ 2/10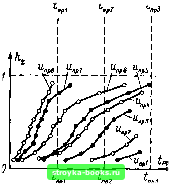

i\ 1 \

- ц,

•по 7

Рис. 4.1. Определение функции поведения напряжения пробоя в длительных испытаниях (схема для 8 уровней напряжения пря rt=10 образцах); а -результаты измерений - пары значений «пр; /пр; б - эмпирическая функция распределения:

* [tap < tnp {) .

Л2 =

в - эмпирическая функция поведения напряжения пробоя прн трех длительностях приложения напряжения - /пр i; /пр г; /пр з

таться с тем, что используемое в эксперименте напряжение должно быть охарактеризовано четко определенными параметрами. Это необходимо учитывать, например, при выполнении длительных (особенно в отношении высокополимерной твердой изоляции) испытаний по определению функции поведения напряжения пробоя (определяют главным образом функцию поведения времени до пробоя при определенном (пробивном) напряжении). При этом длительные приложения переменного напряжения к какому-либо образцу могут служить также для определения функции поведения напряжения пробоя при различной длительности нагрузки (рис. 4.1). Функция поведения напряжения пробоя при различной длительности нагрузки потребуется ниже (§ 5.7) при статистическом изучении эффекта времени.

При исследовании слабонеоднородного поля часто представляет интерес обобщение данных о напряжении пробоя. Случайная величина пробивной напряженности Еар вычисляется при расстоянии между электродами d и коэффициенте

неоднородности tj при случайной величине напряжения пробоя Uap следующим образом:

£np=t/np/(dTi). (4.1)

Если, кроме того, известен коэффициент кривизны е рассматриваемого изолирующего промежутка, учитывающий влияние кривизны электродов на процесс пробоя [25, 192], то в качестве свойства материала может быть введена случайная величина электрической прочности

£np--=t/np-. (4.2)

е аг]е

Естественно, что эта прочность зависит еще и от длительности приложенной нагрузки (см. рис. 4.1, в). Технически целесообразно и вполне оправдано с точки зрения физики процесса описывать случайность процесса пробоя с помощью случайного коэффициента времени [25, 193, 194]

k--El}p(L, (4.3)

Епро

где fnpo -это прочность в течение заданного времени (например, 0=1 мин).

В качестве примера может служить такое приложение импульсного пробивного напряжения, при котором происходящее во времени случайное образование начальных электронов, т. е. случайное, зависящее от времени образование зарядов, проявляет свой случайный характер. Непрерывно меняющиеся удачно выбранные (найденные) случайные величины следует вводить по аналогии с коэффициентом времени kt, если с их помощью может быть удачно описан рассматривающийся случайный процесс пробоя и обобщены экспериментальные данные.

Наконец, часто оказывается удобным рассматривать случайную величину времени до пробоя Т„р. Реализации пр этой случайной величины получают в опытах с заданным напряжением, что позволяет, как и в опытах с нарастающим напряжением (§ 2.3), определить эмпирическую функцию распределения F * (пр) и аппроксимировать ее какой-либо теоретической функцией распределения. В то время как в отношении напряжения пробоя и связанных с ним случайных величин представляют интерес главным образом функции поведения (см. п. 2.1.2), время до пробоя дает исключительно функцию распределения. В особых случаях является даже целесообразным определять функцию поведения времени до пробоя (например, с помощью импульсов равной амплитуды, но различной длительности tup).

Выбор случайной величины Не является Математической проблемой, он должен осуществляться исключительно с точки зрения физики процесса и (или) технической целесообразности и удовлетворительной стоимости выполнения эксперимента.

4.2. Воздушная изоляция

Атмосферный воздух является важнейшим видом изоляции, начиная с низших классов напряжения до сверхвысоких перенапряжений, и поэтому изучен лучше других изолирующих материалов. Слишком большое для полного обзора число публикаций приводит к тому, что ниже могут быть отражены лишь важнейшие моменты, причем исходным пунктом может являться прекрасная монография Мика и Крэггса [195].

4.2.1. Проблемы техники исследований. Атмосферный воздух является единственным изолирующим материалом, который можно рассматривать как полностью самовосстанавливающийся. Изолирующие свойства испытывают влияние климатических колебаний (температуры, давления, влажности). С помощью корректирующих множителей [113, 170] характеристики окружающей среды эксперимента должны быть соотнесены с действующим номинальным напряжением при нормальных условиях (20°С; 101,3 кПа; 11 г/м-з воды). Напряжение пробоя, напротив, обычно должно быть соотнесено с характеристиками при нормальных условиях. Разумеется, стандартизованные корректирующие множители [113, 170] являются эмпирическими величинами, полученными в результате сравнительных измерений во всем мире. Новые широкомасштабные измерения (например, [196-201]), в результате которых должны быть вычислены более точные значения, позволяют решить проблему корректирующих множителей. Различие климатических условий и (еще и сегодня) соответствующих им корректирующих множителей является важной причиной разброса и плохой воспроизводимости результатов.

Развитие разряда зависит от образования в воздухе начальных электронов прежде всего под действием космических лучей, а также ультрафиолетового излучения [25, 202]. По этой причине оба вида излучения явно влияют на напряжение пробоя [194, 203, 204, 205]: напряжение пробоя уменьшается при увеличении интенсивности излучения, особенно в промежутках со слабонеоднородным полем без стабильных частичных разрядов, а также в возмущенном слабонеоднородном

См. также Мик Д. М., Крэггс Д. Д. Электрический пробой в газах. - М.: Изд-во иностр. лит., 1960. (Прим. перев.)