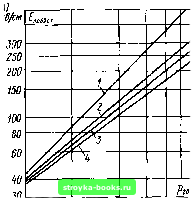кВ/см

0,05 0,1

0.2 0,3 0,4 МПа

О 0.1 0,2 0.3 0,4 0,5М11а

Рис. 4.18. Параметры Япрвзст (а) и (б) двойного экспоненциального распределения при аппроксимации электрической прочности в элегазе

/ - внутренняя электрическая прочность; 2 - переменное напряжение 50 Гц (совпадает с кривой для постоянного напряжения); 3 - отрицательные импульсы коммутационных перенапряжений 250/2500; 4 - отрицательные импульсы атмосферных перенапряжений 1,2/50; для 7 указаны среднее значение и 90 %-ный доверительный интервал

ванйй этого процесса [25, 130, 131, 244] исходят из экстремального распределения напряжения пробоя. Экспериментальная проверка подтверждает (рис. 4.17), что эмпирическая функция распределения электрической прочности значительно лучше описывается не нормальным распределением (рис. 4.17, а), а экстремальными распределениями (рис. 4.17, б и в).

Аппроксимация распределения Вейбулла осложняется тем, что исходные значения Ыпр о или £пр о чрезвычайно зависимы от всех параметров эксперимента, в особенности от трудноопределимой микрошероховатости поверхности электродов и микрочастиц в объеме газа. По практическим соображениям (хорошая аппроксимация, удобство работы, единообразие) наиболее удобно описывать электрическую прочность двойным экспоненциальным распределением [25]. Если для какой-либо серии экспериментов необходимо оценить характеристиками напряжения пробоя, чтобы установить оптимальные значения параметров эксперимента, то в соответствии с рис. 4.18.

Ипр63 = 5пр вЗстТ);

(4.8) (4.9)

где d - расстояние между электродами; г\ - коэффициент неоднородности. Естественно, что эмпирическая функция распре-

0,50 0,30

0,10

0,05

0,03 0,02

¥) 60 80 100

Рис. 4.19. Функция распределения предразрядного времени при импульсах атмосферных перенапряжений в элегазе, аппроксимированная трехпараметри-ческим распределением Вейбулла (вероятностная сетка распределения Вейбулла; радиус коаксиальных цилиндров 0,75 и 2 см; р2о=0,25 МПа; полярность положительная) 7 -начальное значение про" крутизна импульса 5=983 кВ/мкс; 2 - о =220 не; 5=571 кВ/мкс; 3-/„ро=280 не, 5=403 кВ/мкс; 4 - =450 не, S=

=244 кВ/мкс

деления аппроксимируется двойным экспоненциальным распределением и является компромиссом, причем при более высоких давлениях аппроксимация лучше, чем при низких, а диапазон величин остается неограниченным - в противоположность распределению Вейбулла, которое использовалось, например, в работах [72, 142 и 143], несмотря на ненадежность определения исходных значений.

При изучении времени пробоя в элегазе требуется трехпараметрическое распределение Вейбулла (рис. 4.19). Исходное значение /про времени до пробоя пр может быть получено с помощью рассмотрения физики процесса [25]: начальное время /про при известном ходе зависимости напряжения от времени (например, заданной крутизной нарастания напряжения 5 в киловольтах в микросекунду) определяется значением напряжения ы(/про), при котором следует ожидать пробоя при длительном приложении напряжения [см. уравнение (4.8)]. Этот способ легко выполним, и оценка параметров делается

0,95 0,90

а) 0,30 0,80

0,80 0,W

0,20 0,10

0,01

45 55 65 kB/cm 125 135

kB/cm 180 190 200 210 кВ/см

Рис. 4.20. Электрическая прочность промежутка в элегазе при наличии твердого диэлектрика (во всех случаях длина граничной поверхности твердого диэлектрика одинакова; вероятностная сетка двойного экспоненциального распределения); а - для коаксиальных цилиндров с радиусами 5 и 15 см; бив - для коаксиальных цилиндров с радиусами 0,675 и 2 см

еще проще, чем при двухпараметрическом распределении Вейбулла (см. п. 1.3.2).

Равным образом электрическая прочность может быть описана двойным экспоненциальным распределением в элегазо-вых промежутках с сильнонеоднородным полем (рис. 4.20, а, б) при наличии твердой изоляции.

Параметры напряжения пробоя исследуемого промежутка могут быть вычислены с помощью уравнений (4.8) и (4.9), а также значений Япрезст и с рис. 4.21. Если переход между электродом и граничной поверхностью диэлектрика не свободен от нарушений электрического поля, чего следует особенно опасаться при высоком давлении в элегазе, то аппроксимация электрической прочности и напряжения пробоя с помощью нормального распределения часто является более точной (рис. 4.20, в). Если тем не менее выполнять аппроксимацию двойным экспоненциальным распределением, то возникает ошибка в «безопасную сторону».

4.3.3. Элегазовая изоляция в возмущенном сильнонеоднородном поле. Конструируемое слабонеоднородное поле в сжатом газе нельзя получить при наличии ошибок монтажа, приводящих к частичным разрядам. Подобные дефекты поля могут быть неподвижными (острые края, грани, заусеницы, щели) или двигаться под действием сил электростатического поля