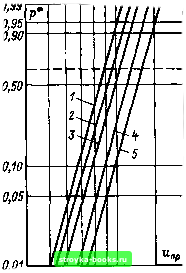ио 50 SOW 90100 150 кВ

Рис. 4.26. Распределение Вейбулла напряжения пробоя промежутка плоскость - плоскость в трансформаторном масле при различной длительности приложенного переменного напряжения [73]

/-длительность воздействия 10 ч; 2 - 1 ч; 3-10 мии; 4-1 мии; 5-10 с

эксперимента и (или) совмещение весьма большого числа серий измерений может привести к заключению о нормальном типе распределения (256] и установлению его параметров. Нормальное распределение следует использовать только для приближенного описания и для промежутков с сильнонеоднородным полем. Некоторые значения коэффициентов вариации при пробое

промежутков в минеральном масле приведены в табл. 4.6.

В американской литературе экстремальные распределения, описывающие проблемы масляной изоляции, использовались уже в пятидесятых годах [68-75]; этот случай описан в качестве типичного в классической книге по статистике [39]. Новые публикации возвращаются к этим работам и используют как двойное экспоненциальное распределение [260], так и распределение Вейбулла [54, 73]. Весьма большая дисперсия пробивных напряжений в изолирующем масле приводит к тому, что уже двухпараметрическое распределение Вейбулла очень хорошо подходит для аппроксимации [73]; в практике измерений трехпараметрическое распределение Вейбулла (см. п. 4.3.2) не является безусловно необходимым. Интересно, что длительность нагрузки не влияет на показатель экспоненты Вейбулла, т. е. на крутизну функции распределения (рис. 4.26). Эта тенденция подтверждается и для электродов с покрытиями [260]. Распределение Вейбулла успешно используется как для описания масляных изолирующих промежутков, так и для бумажно-масляной изоляции [260-262], и дает возможность единого описания этого типа изоляции. Поскольку часто масляная изоляция может изучаться лишь на малых моделях, большую роль играет правильность их соотнесения с крупными техническими изделиями (например, изоляция трансформатора) с помощью закона преобразования масштаба (см. гл. 5). Экстремальные распределения и в этом случае раскрывают благоприятные перспективы. По этим причинам распределение

Вейбулла (или двойное экспоненциальное распределение) рекомендуется для описания пробивных напряжений в масляной изоляции в слабонеоднородных и однородных электрических полях.

4.5. Твердея изоляция

Электрическая прочность твердых изолирующих материалов может достигать значений 1000 кВ/см и выше, однако она настолько сильно зависит от состояния изоляции, что в технике редко может быть использовано значение свыше 100 кВ/см. Кроме того, изолирующие свойства органической и неорганической изоляции заметно меняются в зависимости от длительности нагружения напряжением: в то время как для неорганических изолирующих материалов (например, фарфор, стекло) имеет место относительно слабая зависимость от времени нагружения, эта зависимость настолько велика для создаваемых органических изолирующих материалов (например, эпоксидной смолы, полиэтилена и др.), что ее называют «кривой жизни» [216]. По этой причине время до пробоя, как

с0,99

0,95 0,90 0,80 0,70 0,60 0,50

0,30 0,20

0,10

0,05 (1,04 0,03

0,02

Ь) 0,99

0,90

0,80 0,70 0,60 0,50 0,40 0,30 0,20

0,10

0,05

10 10

10"

ю ю ю

10 10

10° Ю 10 ю" V

Рнс. 4.27. Аппроксимация функции распределения времени до пробоя в отрезке кабеля с полиэтиленовой изоляцией [263]: а - аппроксимация двухпа-раметрнческим распределением Вейбулла (вероятностная сетка распределения Вейбулла); б - аппроксимация логарифмически нормальным распределением (вероятностная сетка логарифмически нормального распределения); напряжение пробоя при переменном напряжении «пр = 49 кВ; радиусы коаксиальных цилиндров 1,5 и 3,5 мм, длина 1 м

и напряжения пробоя, являются важнейшими случайными величинами при оценках свойств изоляции. В дальнейшем изложение ограничено исследованием высокополимерных изолирующих материалов ввиду их благоприятных свойств, имеющих преобладающее значение в настоящее время и в будущем. Целесообразно также включить в рассмотрение и другие органические изолирующие материалы (например, бумагу), а также исследовать развитие разряда вдоль органических поверхностей, при котором на поверхности твердого тела имеют место термические и плазмохимические реакции.

В опытах с неизменным напряжением (см. п. 2.2.3 и § 4.1) определяют функцию распределения времени до пробоя (рис. 4.27), которая, как правило, аппроксимируется двухпа-раметрическим распределением Вейбулла или нормальным логарифмическим распределением (см. п. 1.3.2). Опыт последних лет явно указывает на то, что с точки зрения математики распределение Вейбулла предпочтительнее нормального логарифмического распределения, когда должен быть выполнен пересчет на основании соотношений времени до пробоя (см. п. 4.5.2) или закона преобразования масштаба (см. гл. 5). Кроме того, модель на основе экстремального распределения является более предпочтительной и из физических соображений, когда электрический пробой распространяется в твердом теле с какого-либо (экстремального) острия.

Функцию суммарной частости и функцию поведения напряжения пробоя также удобно описывать распределением Вейбулла (рис. 4.28), хотя существует и принципиальная возможность аппроксимации логарифмическим нормальным распределением.

Если внешние условия эксперимента заметно меняются (см. п. 4.5.1), может получиться, что измеренные пробивные напряжения распределены нормально. Свойства случайного процесса проявляются в этом случае в меньшей степени, нежели свойства внешних условий.

Как и для жидкой изоляции, в дальнейшем могут быть сделаны лишь указания по технике эксперимента и решению основных проблем статистики. Указания по предварительной оценке функции распределения напряжения пробоя и времени до пробоя носят недостаточно общий характер, чтобы их можно было привести в имеющемся объеме материала. Как правило, действуют на основании предварительных экспериментов (например, при исследовании времени до пробоя -на основании предварительных кратковременных испытаний).

4.5.1. Проблемы техники исследований. Каждый электрический разряд приводит к необратимым нарушениям структуры твердого тела, т. е. твердые изолирующие материалы не являются самовосстанавливающимися. Поэтому для каждого