чины Xi, большие установленных уровней, однако проще, как показано в табл. 1.2, рассортировать все реализованные величины Xk = u„pk. Ручная обработка таблицы первичной реализации при больших объемах выборки чрезвычайно трудоемка. Для уменьшения объема расчетных работ выделяют величины Xk в диапазоне от Хтш до хах и для них определяют частости. Таким способом образуется таблица частостей. Перед тем как приступить к ее построению, тщательно проверяют, чтобы переход от таблицы первичной обработки к таблице частостей происходил без потерь информации.

Всегда, когда объем расчетов не имеет большого значения (например, при малом объеме выборки или при использовании ЭВМ), следует отказываться от построения таблицы частостей и выполнять дальнейшие оценки по таблице первичной обработки.

Необходимые для таблицы частостей размеры интервалов деления можно получить в результате следующей оценки: число ступеней k желательно иметь между 7 и 20, для чего принимают

А: = 5 In п. (1.37)

После установления числа интервалов k следует по величине промежутка

R=Xmaii - Xin (1.38)

определить длину интервала

R/k.

(1.39)

Выходное значение Хщ (нижняя граница первого интервала) должна быть меньше наименьшей суммарной величины ixiu< <-min) и d должно быть тзким, чтобы ни одна из границ ин-

Табшца 1.3

тервалов не совпадала с какой-либо измеренной величиной. Желаемое число интервалов k и начальное значение Х\п устанавливают эмпирическую функцию распределения. Насколько неопределенным является построение этих интервалов, видно по изображенным на рис. 1.4 эмпирическим функциям распределения, которые все построены по одному протоколу из при-

0,80

0,60

0,20 0.

по 180 190 200 210 кВ

Рис. 1.4. Эмпирические функции распределения, построенные на основании

примера 1.12

/ - по табл. 1.3 при *=7; d=6 кВ; «пр 1и°°* 2 - при ft=10; d=5 кВ; "пп 1н ~ = 170.5 кВ; 3-при *=?; d=7 кВ; Unpj„=170,5 кВ; < -по табл. 1.2

мера 1.12 и, несмотря на это, существенно отличаются одна от другой.

Пример 1.14. Согласно примеру 1.12 к=Ъ Ig 24=6,9011; заданные k=7; /? = 216-175 кВ = 41 кВ; d=R/k=4l кВ/7=5,8571; положим d=6 кВ. Начальное значение «пр ih= 174,5 кВ.

В таблицу частостей (табл. 1.3) сведены интервалы, число реализаций в каждом интервале и частости (1.35)-(1.36).

Для инженерной обработки эмпирической функции распределения ее графическое изображение непригодно. Одновременно с таблицей первичной обработки (табл. 1.2) эмпирическая функция распределения может быть изображена в виде ступенчатой кривой, кривой суммарной частости и полигона суммарной частости, как, например, в табл. 1.4. Приведенные здесь графические изображения с помощью линейной шкалы ординат используются относительно редко. Чаще используют подходящую вероятностную сетку, на которой шкала ординат

Вид изображения

Способ получения изображения с помощью

таблицы распределения (табл. 1.2)

таблицы частостей (табл. 1.3)

Пример изображения

Ступенчатая кривая

Суммарные частости ftfe [см. формулу (1.36)1 изображаются ступеньками с шириной, равной минимальному изменению аргумента [Дл; = = min (л;,+1 - л;)], меняющегося в пределах, заданных таблицей: х = Xk

Суммарные частости Л/ изображаются в виде ступенек на всех интервалах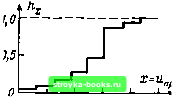

175 185 195 205 215 кВ

Полигон суммарной частости (особенно рекомендуется!)

Значения суммарных частостей ftsfe изображаются точками с ординатами, соответствующими реализациям xi, и соединяются ломаной линией; каждая реализация отображается одной точкой

Суммарные частости Л; изображаются точками, соответствующими верхним границам интервалов аргумента, и соединяются ломаной линией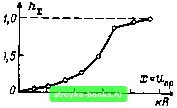

175 185 195 205 215

Кривая суммарной частости

Суммарные частости /г наносятся так же, как для построения полигона суммарной частости, и по ним проводят плавную кривую

Суммарные частости hi наносятся так же, как для построения полигона суммарной частости, и по ним проводят плавную кривую

175 185 195 205 215 кВ

Примечание. 1. Ступенчатая кривая является прямым эмпирическим аналогом функции распределения (1.13) - см. также выражения (1.1) и (1.36). Для технических задач часто удобнее использовать полигон и кривую суммарной частости, которые могут быть построены с помощью выражений (1.35) и (1.36).

2. При использовании вероятностной сетки кривые превращаются в прямые линейной регрессии (см. § 1.4).