
 |
|
Главная Среднее значение величин [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [ 82 ] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] ответствующем значении /ж о, например, равном 0,01, и оценочной величине ы*пр.нр для «пр. hp начальное напряжение «про = "пр.нр У 1жо- (4.19) Для использования описанной схемы пересчета с помощью уравнений (4.17) и (4.18), безусловно, необходимо знать точное значение г во всем рассматриваемом диапазоне кривой длительности жизни и для всех квантилей функции распределения. Если на кривой длительности жизни имеется излом, то с уравнением (4.17) работать нельзя. Если все условия выполнены, то функция распределения пробивного напряжения в опытах с неизменным напряжением может быть определена с большой точностью в расчетах времени до пробоя, проведенных в опытах с нарастающим напряжением в соответствии с формулой (4.17) (рис. 4.38). Соответствие является особенно хорошим в диапазоне средних значений, как это показано на рис. 4.39. 4.6. К статистике частичных разрядов В условиях постоянного увеличения степени использования для расчетов электрической прочности изолирующих материалов измерения заряда частичных разрядов играют все более возрастающую роль [25, 283-285]. С помощью современных систем измерения частичных разрядов (например, [286, 287]) можно измерять различные характеристики (заряд в импульсе, максимальное значение импульсного заряда, а также кажущийся заряд, суммарный заряд, среднее значение тока частичного разряда, энергию частичного разряда, частоту импульсов и т. д.), которые без исключения следует рассматривать как случайные величины (как и «средние» величины). В рамках данной книги могут быть сделаны лишь наиболее существенные замечания относительно статистики частичных разрядов, касающиеся наиболее важной измеряемой величины - заряда импульса (кажущегося заряда). При этом особенно необходимо учитывать взаимодействие между случайным процессом и измерительной цепью [287, 288]. В большинстве устройств для измерения частичного разряда может быть установлен рабочий интервал времени (время чувствительности), начинающийся в заданную фазу испытательного напряжения и обладающий заданной длительностью (рис. 4.40, а, б). Случайный процесс разряда возбуждает в измерительной цепи [283, 286] протекание тока, состоящего, как правило, из импульсов тока со случайным значением, длительностью, зарядом и частотой следования (рис. 4.40, в). Импульсный заряд (область под времятоковой характеристикой ji Начало частичных! I разрядоб частичных разрж) 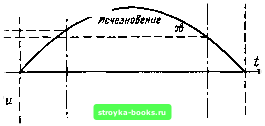
 , I Максимальный импульсный заряд lilillllliiiii Рнс. 4.40. Измеряемые характеристики импульсных разрядов (схема) импульса) определяется с помощью электронного измерительного устройства; система генерирует соответствующий импульс, заряд и амплитуда которого пропорциональны импульсному заряду частичного разряда (рис. 4.40, г). Форма этого импульса меняется в зависимости от используемого принципа измерений: чем в более узкой полосе работает система измерения заряда частичного разряда, тем длиннее этот импульс по сравнению с исходным импульсом тока. Даже в широкополосных устройствах длительность генерируемого импульса больше, чем исходного [286]. По измерениям отдельных импульсных зарядов может быть определена функция распределения. Поскольку оценка получающихся осциллограмм весьма трудоемка и подвержена ошибкам, используют импульсные анализаторы [288]. Они одновременно оценивают импульсный заряд и частоту импульсов как меру интервала времени между двумя импульсами заряда. В качестве абсолютного распределения частот в известной 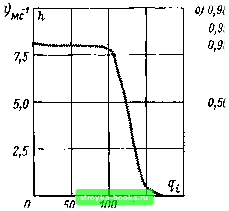 150 пКл 0,10 0,05 0,02 80 120 160 пКл Рис. 4.41. Функция распределения импульсных зарядов [288] в воздушном промежутке стержень - плоскость: а - результаты измерений с помощью анализатора импульсов; б - функция распределения (2) и частость превышения заданного уровня (/) (вероятностная сетка нормального распределения) степени принимают взаимосвязь между импульсным зарядом и абсолютной частотой следования импульсов, причем в эксперименте задаются заряды и может быть определена частота возникающих импульсов заряда этого уровня. Несколько реже, руководствуясь этой экспериментально определенной кривой, изображают функцию распределения импульсного заряда F{qi) (рис. 4.41, б, кривая 2) как дополнительную к ней частость превышения заданного уровня (рис. 4.41, б, кривая 1) Во многих случаях для функции F{qi) может быть принято нормальное распределение, если прежде всего имеет место отдельная точка образования частичного разряда. Естественно, что особый интерес представляют интенсивные импульсные разряды, когда функция Hdqi) связана с малой вероятностью, а F(qi) представлена большими квантилями. При этом использование функции Яс(<7г) технически наглядно, а f ((7,) - математически удобно. При известном навыке не остается сомнений в том, что следует работать непосредственно с функцией распределения F{qi). Максимальный импульсный разряд можно, с одной стороны, как уже отмечалось, характеризовать как квантиль [288], а с другой стороны, видно, что он же является величиной, измеряемой в большинстве систем измерения частичных разрядов, и необходим в качестве полезной информации (см. рис. 4.40, г, [286]). Информация от измерительного устройства представляется при этом значением, усредненным по большому [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [ 82 ] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] 0.0012 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||