изоляции за счет связанной с разрядами поверхности (эффект площади) или объема (эффект объема), а также влияния увеличения длительности нагрузки (эффект времени).

5.2. Статнстические основы

Для статистического описания увеличения или уменьшения протяженности испытаний в пространстве (объем V) или во времени (время Т) вводят четырехмерный множитель п, который при переходе к новому состоянию (F„, Тп) из исходного состояния (Fl, Tl) имеет вид

«=-f (0<n<-foo). (5.1)

В дальнейшем будем основываться прежде всего на этом масштабном множителе га, причем естественно оказываются охваченными все частные случаи трех-, двух- и одномерных масштабных множителей, как при изменении объема (n=V„/Vi; 7„ = 7i), изменении площади («=/4„ 4i = F„/Fi; Tn = Ti), изменении времени (п=7„/7г, "„ = 1) или при параллельном включении отдельных изоляторов (л - число параллельных изоляторов).

При увеличении изоляции с вероятностью пробоя pi = Fi{xo) с масштабным множителем п под действием нагрузки Хо (например, Xo = Uo) новая вероятность пробоя p„ = Fn{Xo) определяется непосредственно законом умножения вероятностей (1.12), в котором рассматривается дополнительное событие отсутствия пробоя. Отсутствие пробоя в увеличенном промежутке (1-рп) означает отсутствие пробоя во всех исходных промежутках (1-Pi),-, t=l, 2,..., п:

(l-p„) = (l-Pi),(l-Pi)2 . . . (1-Pi)«, (5.2)

что при {\-pi)i= (1-jOi)2= ... = (1-Pi)n дает

p„=l-(l-Pi)«. (5.3)

Если рассматривать не только дискретные значения вероятностей, но всю функцию распределения Fi{x) или F„(x), то получим

FAx)=\-[l~F,ix)r. (5.4)

До этого момента при изменении масштаба всем п элементам приписывались идентично распределенные случайные характеристики. На практике,, однако, это не всегда так. Например, вероятности пробоя различны {Рч при t=l,..., га), если при увеличении объема имеет место изменение распределения напряженности электрического поля хотя бы вследствие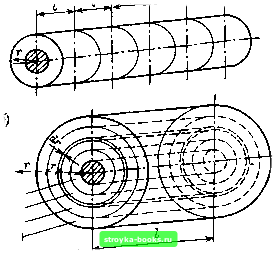

Va=hiF,,(x)=1-n[1-F(x)J

Рис. 5.1. Преобразование размеров коаксиального кабеля: а - увеличение длины; 6 - увеличение радиуса

изменения радиусов коаксиальных систем. Уравнение (5.2) приобретает вид

(1р„) = (1-рО(1-Р2)...(1-Рг) (1 = 1,..., п), (5.5)

откуда для разделенных изоляторов общая форма закона преобразования масштабов примет вид

/п=1-П (1-PiO

п()=1-П ll-Fii(x)].

(5.6)

(5.7)

Использование формул (5.3), (5.4), (5.6) и (5.7) не представляет затруднений при разделенных изоляторах (см. § 5.4), если известны или Рц{х). Прн протяженной изоляции

использование этих соотношений требует более нли менее произвольной дискретизации. Например, для коаксиального кабеля увеличенной длины это достигается разделением его на п одинаковых частей (рис. 5.1, а) с одинаковой вероятностью

пробоя, что представляет, однако, существенные затруднения, если при изменении масштаба произошло изменение распределения напряженности поля. Если коаксиальный промежуток постоянной длины увеличивается в радиальных размерах, необходимо сделать выбор цилиндрических объемов различных размеров (рис. 5.1, б), обладающих, естественно, различной вероятностью пробоя. В таких случаях выгоднее отказаться от произвольной дискретизации и использовать интегрирование по объему. В качестве элементарного объема можно принять произвольный элемент объема Vi в однородном поле при произвольно выбранной длительности нагрузки Ti (исходные значения ViTi). Любое неоднородное поле из-за присущей ему неоднородности распределения напряженности непригодно в качестве элемента для преобразования или сопоставления.

пример 5.1. Пусть измеряется напряженность пробоя на коаксиальной модели полиэтиленового кабеля с отличающимися от оригинала внутренним радиусом, длиной и толщиной изолирующего слоя. В соответствии с описанной ниже методикой эмпирическая функция распределения различных моделей кабеля может быть приведена к функции распределения единичного элемента в однородном поле с объемом, например, Vi = \ см. Вычисляемые параметры функции распределения для Vi сравниваются между собой. Исходя из определенной таким способом функции распределения для Vl можно вычислить функцию поведения произвольной изоляции, если верна используемая статистическая модель.

Единичному элементу (ViTi) соответствует функция распределения используемой случайной величины X с параметрами а и р, неизвестная первоначально и определяемая затем способом, указанным в примере 5.1 (см. § 5.6):

FAx) = F,(x; а; Р).

Произвольному бесконечно малому элементу величиной dvdt в рассматриваемом неоднородном поле соответствует случайная величина Хе, имеющая важную физически осмысленную связь со случайной величиной X, характеризующей единичный элемент. Это в особенности подходит к случайным значениям пробивной напряженности электрического поля Х=Ещ,тах и электрической прочности Х=£пр [25]. В целом связь между Хе и X должна осуществляться с помощью специальной функции геометрии и (или) времени в форме f{v\ t):

X, = Xfiv; t) = X,(U„p; v; t). (5.8)

В дальнейшем показано, что случайная велична Хе распределена идентично характеристике единичного элемента X, т. е. что для дифференциального элемента пригодна функция F{Xe; а; Р) с Хе, удовлетворяющим условию (5.8). Полный промежуток состоит из бесконечно большого числа дифференциальных элементов, каждый из которых необходимо учесть.