0,9999

0,9995

0,998

0,995

0,99

0,95

0.1 0,05

0,01 0,005 0,001 0,0005

0,0001

«5>-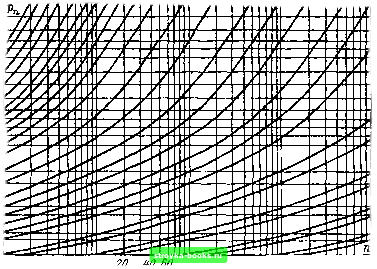

0,0005

0,0001 0,00005

0,00001 0,000005

0,000001 0,0000005

0,0000001 0,00000005

6 810

100 200

1000 2000 WOO 10000

Рис. 5-11. Зависимость вероятности пробоя от числа одинаковых параллельно включенных элементов [40]

на составляющие (например, нормальные распределения), то по отношению к каждой из них могут быть использованы закономерности, найденные для функций распределения [40].

Так называемые мультипликативные распределения [69] получаются непосредственно при использовании закона преобразования масштаба [например, (1.14) и (1.17)]. Они поэтому не являются фундаментальными исходными распределениями, но сами составляются на их основе. Для них, как и для всех других функций распределения, функция распределения преобразованного промежутка определяется либо полным расчетом по формуле (5.4), либо по точкам в соответствии с уравнением (5.3), а лучше - с помощью номограммы (рис. 5.11), приведенной в § 5.4.

5.4. Взаимно независимые параллельно включенные разрядные промежутки

При параллельном включении взаимно независимых разрядных промежутков масштабный коэффициент является одномерным и равен известному числу промежутков п. В качестве объекта исследования может быть рассмотрена, с одной стороны, любая изоляция, состоящая из отдельных элементов (параллельно включенных изоляторов, изоляции параллельных обмоток и т. д.), а с другой стороны - любая протяженная изоляция, допускающая недвусмысленную дискретизацию (кабели, коаксиальные сборные шины в оболочке и др. при увеличении длины), причем для последней в качестве единичного элемента можно использовать любой удобный для экспериментального изучения отрезок (например, в лабораториях выделяют отрезок кабеля длиной 2 м). Если, как при увеличении площади и объема, подобная дискретизация возможна, то такой путь является предпочтительным, что сильно упрощает расчеты.

При параллельном включении одинаковых элементов используют уравнения (5.3) и (5.4). Для очень малых вероятностей пробоя (р1<1/п) более детальные выкладки [40] приводят к простому выражению для полномасштабной изоляции

Рп = прг (5.21)

f „ (jc) = nf 1 (jc) в диапазоне fi(je)< {In. (5.22)

Использование этого подхода [уравнения (5.3) или (5.21)] изображено на рис. 5.11, с помощью которого при заданной вероятности пробоя единичного элемента (Pi) можно определить вероятность пробоя при пЮ* параллельно включенных элементах. Вероятность рп относится к полному промежутку и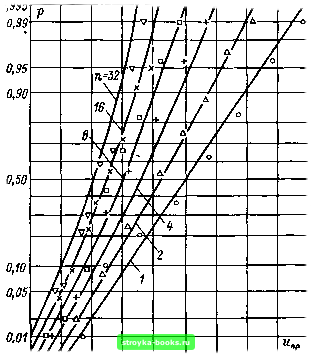

198 201 204 207 210 213 216 219 222 кВ

Рис. 5.12. Эмпирическое исследование действия преобразования масштаба при параллельно включенных искровых воздушных промежутках [40] острие-плоскость (длина промежутка 40 см; импульсы атмосферных перенапряжений 1,2/50)

определяется пробоем любого числа элементов, хотя можно с уверенностью считать одновременный пробой двух или более элементов чрезвычайно маловероятным [292].

Использование этих соотношений позволяет прежде всего определить функцию распределения л параллельных элементов по данным об одном элементе. При этом для искровых промежутков типа острие - плоскость закон преобразования масштаба используется на основании нормального распределения (рис. 5.12), а для параллельно включенных изоляторов в вакууме следует исходить из распределения Вейбулла [293].

Особенно важной проблемой при разработке кабелей и герметизированных сборных шин является разделение коаксиального цилиндрического промежутка на элементы длиной /ь которые при наращивании длины включаются параллельно (л= = /„ i). При моделировании кабеля с полиэтиленовой изоля-