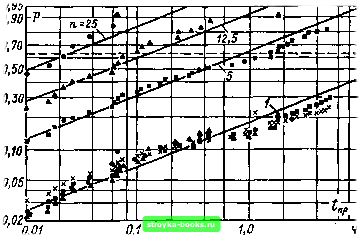Рис. 5.13. Увеличение длины кабеля с полиэтиленовой изоляцией: преобразование масштаба по отношению к случайной величине времени до пробоя, распределенной по закону Вейбулла Радиусы коаксиального кабеля 1,5 и 3,5 мм; длина кабеля /[ = 1000 мм

цией возможность использования закона преобразования масштаба была подтверждена на основе распределения Вейбулла для напряжения пробоя и времени до пробоя (рис. 5.13), в то время как в отношении электрической прочности элегазовой изоляции коаксиальных цилиндров следует исходить из двойного экспоненциального распределения (рис. 5.14) [40, 69 и др.].

Далее, существует возможность обращения соотношений, при котором функция распределения единичного элемента Fl (х) выражается через функцию распределения п параллельно включенных элементов Fn{x):

FAx)l-Vl-Fn(x).

(5.23> (5.24).

Если вероятность пробоя изоляции должна быть определена вплоть до весьма малых значений, рекомендуется исследовать п параллельно включенных изоляторов и затем перейти к расчету параметров изоляции с помощью уравнений (5.23) или (5.24).

Пример 5.2. Необходимо определить функцию распределения промежутка стержень - плоскость (d=40 см) при атмосферных перенапряжениях вплоть до значения pi = 0,0005. Для этого требуется ие менее /=2000 нс-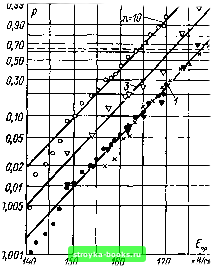

Рис. 5.14. Преобразование масштаба при удлинении коаксиального цилиндрического промежутка в элегазе (радиусы коаксиальных электродов 6 и 20 мм, длина 1\ = = 10 мм)

пытаний. Затраты будут существенно уменьшены, если иа основе изображенной на рис. 5.12 эмпирической вероятности пробоя (/=100) для п, равных 32, 16, 8, 4 и 2, параллельно включенных искровых промежутков выполнить пересчет к одному промежутку с помощью формулы (5.23) (рис." 5.15). Естественно, существует принципиальная возможность при расчетах соотнести параметры нескольких параллельно включенных элементов (например, /1=32) с параметрами одного промежутка. При этом удобно использовать рис. 5.11. Для контроля точности следует получить границы доверительного интервала вероятности пробоя (см. п. 1.3.1) с помощью уравнения (5.23), например, для /1=32 искровых промежутков при /=100 и сравнить их с непосредственно определенными при /=2000 границами.

Сопоставление эмпирически определенных коэффициентов вариации для одного и п параллельно включенных изоляторов может быть также использовано для определения типа распределения [294]. При этом требуется предварительно определить соотношения между коэффициентами вариации при параллельном включении нескольких элементов - ип = 5п/л:п и для одного элемента v\ = s\lxi для различных теоретических функций распределения (табл. 5.2 и графики рис. 5.16), а затем проверить, какой теоретически определенный ход Vn = f(n) описывает эмпирически найденные величины наилучшим образом.

Пример 5.3. При исследовании времени до пробоя параллельно включенных искровых промежутков между остриями в зависимости от масштабного коэффициента были получены следующие коэффициенты вариации:

Масштабный коэффициент п Коэффициент вариации и„

0,175

0,078

25 0,048

Сопоставляя эти значения с теоретически найденными зависимостями (рис. 5.16 и табл. 5.2) замечаем, что эмпирическая кривая Vn=fn лучше всего описывается трехпараметрнческим распределением Вейбулла. В исследуемых искровых промежутках время до пробоя описывается распределением Вейбулла.

0,995 0,99 0,98

0,95 0,90

0,80 0.70 0,80 0,50 0,W 0,30

0,20

0,10 0,05

0,02 0,01 0,005

0,002 0,001 0,0005 0,0002,

198 201 204 207 210 213 216 219 222 кВ

Рис. 5.15. Эмпирическое определение функции поведения искрового воздушного промежутка по п параллельным промежуткам (рис. 5.12)

С Практической точки зрения существенное значение представляет параллельное включение различных типов изоляции - например, различных изоляторов в выключателях нли обладающих различной изоляцией обмоток трансформаторов [295], причем задача может быть решена только на основе уравнений (5.6) и (5.7). В частном случае параллельного включения двух изоляторов с вероятностями пробоя Рп и Pi2 результирующая вероятность пробоя может быть определена по номограмме рис. 5.17 (например, при pii = 0,05; pi2 = 0,15 получаем Р2 = = 0,20).