Рис. 5.16. Зависимость коэффициента вариации On=(s/x)„ от коэффициента преобразования масштаба п при различных теоретических функциях распределения [294] (при б= = 1,7 сильнее всех меняется трехпараметрическое распределение Вейбулла)

/ - двойное экспоненциальное распределение; 2 - двухпараметрическое Вейбулла; 3 - нормальное; 4 - трехпараметрическое Вейбулла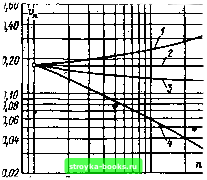

В ею 20 30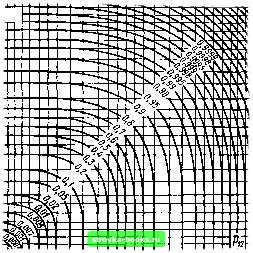

4Ssf

0,9999998 0.9999995 11,999999 0,999998 0,999995 0,99999

0,99998 0,99995

Рис. 5.17. Вероятность пробоя при параллельном включении двух различных

элементов [40]

5.5. Влияние на пробой изменения площади поверхности изолятора

(Электрический заряд развивается при критической пробивной напряженности неоднородного поля в определенном объеме, который определяется, с одной стороны, поверхностью электродов (т. е. частью поверхности с достаточно высокой напряженностью), а с другой стороны - длиной силовой линии Ах (рис. 5.18). Если длина Ах мала по сравнению с расстоянием между электродами d или если напряженность меняется вдоль пути разряда слабо, то от рассмотрения «пространственного пробоя» можно перейти к «поверхностному пробою». В этом случае вместо математического исследования влияния на пробой объема изолятора можно изучать влияние площади поверхности.

Представления о влиянии на пробой площади поверхности изолятора подтверждаются экспериментами в слабонеоднородном поле, главным образом, для тонких слоев твердых и жидких диэлектриков. Они пригодны, например, для пленочных изоляторов в конденсаторах, кабелях, вводах [65, 291, 296, 297], а также и для масляных каналов в трансформаторах [35, 75, 298] (рис. 5.19), причем описание напряжения пробоя можно

0.995 0,99 0,98 0,95 0,90

0,80 070 (f,60

0,30 0,20

0,10 0,05 0,02 0,01 0J05 (1,002 0,001 0,0005 0,0001

Рис. 5.18. К определению влияния иа электрическую прочность изменения площади и объема-, а - влияние объема (твердый диэлектрик); б - влияние площади поверхности при Ax<d и £»£пр (сжатый газ); в - влияние площади поверхности при £»const (тонкий слой изоляции)

d - изолирующий промежуток; х - критическая длина лавины

производить нормальным, двойным экспоненциальным распределением или распределением Вейбулла. Кроме того, модель влияния на пробой изменения площади поверхности особенно хорошо зарекомендовала себя по отношению к сжатым изолирующим газам в слабонеоднородном поле [70- 72, 76, 77, 2991, где приводящая к пробою критическая лавина развивается на пути длиной, возможно, менее 1 мм. В первую очередь поэтому оказывается при-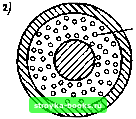

Рабномто распределенные дефекты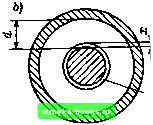

~ Объем зарождения разряда

годным использование двойного экспоненциального распределения (рис. 5.20) и распределения Вейбулла.

При математическом описании влияния на пробой измене-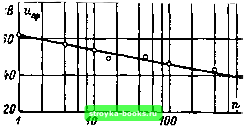

1000

Рис. 5.19. Эмпирическое исследование влияния изменения площади поверхности в изоляционном масле (вероятностная сетка двойного экспоненциального распределения) {75]