=2nri{l-li)fAi и n3=2nri/Ai. В области ввиду того, что £iip3=£np(2) [см. (5f.29)], «масштабный коэффициент» зависит от случайной величины:

«2 =

Al У 0,268£пр )

( 0.268

(5.35)

Вычисления по этой формуле показывают, что в диапазоне 140 кВ/см< <£пр<180 кВ/см масштабный коэффициент Яг в области лежит между 10,0 и 7,8 и явно меньше, чем л,=62 770 и Лз=63. В то время как обычно случайную характеристику, зависящую от масштабного коэффициента, необходимо вычислять по формуле (5.35), в данном случае следует вести вычисления приближенно с постоянным значением масштабного коэффициента «2=8,8 (чисто геометрически получается «2=63). При этом выражение (5.34) приобретает форму (5.14) и, таким образом, при параллельном включении элементов, электрическая прочность которых описывается двойным экспоненциальным распределением с различными параметрами,

fn (£.,) = 1 - в.р [- ехр - «Р (-5=)-

(5.36)

Графическое изображение этих соотношений показывает (рис. 5.22), что в диапазоне длительно допустимого напряжения функция распределения

0,99

0,90

0,70

0,50

0,30 0,20

0,10 0,05

0,01 0,005

130 140 150 160 170 180 кВ/ш

Рис. 5.22. Влияние поверхности в элегазовом промежутке (пример 5.4) / - полный промежуток „=628 956 см); 2 - цилиндрическое поле (/li=627 700 см); 3 - сферическое поле (Аг=Ъ2Ъ см); •< -переходный участок (Л2=628 см); 5 -исходный элемент с однородным полем 4о-10 см«

переходной области не оказывает почти никакого влияния на Fn( П6-9тому формулу (5.36) можно упростить:

fn (Япр) = 1 - ехр [- ехр (е) - ехр (f)

. (5.37)

Поскольку двойное экспоненциальное распределение утеряно, обладающая большой поверхностью область / из-за большой дисперсии определяет малые квантили, в то время как средние значения явно испытывают влияние полусферической области /П. Полученный результат может быть использован для улучшения исходной системы, в особенности для области 1{г\1гг=е= =2, 7,...) и для выбора формы участка / [25].

Пример ЯВНО показывает, что влияние на пробой площади поверхности при напряженности, неравномерно распределенной вдоль поверхности, будет описываться функцией распределения, которая более не соответствует введенным теоретическим функциям распределения, трудна в обращении и не наглядна. Поскольку это влияние имеет большое значение для газоизолированных систем со слабонеоднородным полем, уравнение (5.25) следует использовать при расчетах с помощью ЭВМ.

Сходный в своей основе, но не вполне последовательный по выполнению путь учета влияния на пробой площади исследован в работах [70, 71]. Рассматривается распределение напряженности вдоль поверхности, и в отношении наиболее нагруженной полем части поверхности используется закон преобразования масштаба в обычной форме. При таком подходе исключается возможность зависимости масштабного коэффициента от напряженности [см. уравнение (5.35)].

Во многих случаях результаты такого подхода соответствуют полученным выше, однако в некоторых частных случаях (например, при описании электродов сложной формы в коаксиальной системе [25]) при этом методе следует опасаться ошибки.

5.6. Влияние на пробой изменения объема изоляции

Если развитие разряда, приводящее к пробою, не может быть, как описано выше, изображено зависящим лишь от площади поверхности, а носит выраженный пространственный характер, необходимо рассматривать эффект преобразования масштаба по отношению к объему. В особенности тщательно это явление изучалось для изоляции технически чистым маслом в большом объеме (рис. 5.23) [35, 68, 73, 258, 259, 291, 294] и прежде всего для твердой высокополимерной изоляции [64, 300], где частички могут быть распределены по всему объему изоляции.

Если увеличение объема изолирующего промежутка происходит в плоскопараллельном поле в осевом направлении (на-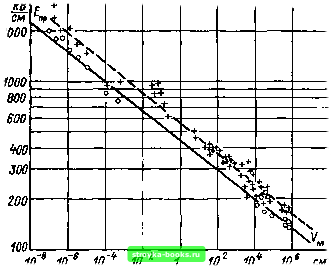

Рис. 5.23. Эмпирическое исследование влияния изменения объема Км на электрическую прочность изоляционного масла (вероятностная сетка распределения Вейбулла) [73] Светлые точки - коммутационные импульсы; крестики - грозовые импульсы

Пример, как показано на рис. 5.1, а при удлинении отрезка кабеля), это не окажет влияния на распределение напряженности и можно разделить полный промежуток на технически удобные участки. Необходимо лишь добиться того, чтобы развитие разряда на этих участках не оказывало взаимного влияния. При подобном увеличении масштаба можно работать лишь с дискретными элементами (см. § 5.4), используя известные соотношения между теоретическими функциями распределения (см. § 5.3).

Существенную сложность представляет увеличение объема изоляции, при котором происходит изменение распределения напряженности. Обобщенный закон преобразования масштаба (6.11) принимает вид

] ln[l-F(x,; а; )]dv\. (5.38)

f„()=l-exp

Случайная характеристика Хе малого элемента объема dV= =dudydz будет произведением случайной характеристики X единичного элемента V\ и геометрической функции; для их реализаций имеет место

x, = xf{u\ у; г). (5.39)