
 |
|
Главная Среднее значение величин [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [ 93 ] [94] [95] [96] [97] [98] [99] [100] [101] Для определения геометрической функции следует выбрать подходящую систему координат. Пример 5.5. Электрическую прочность полиэтиленовой изоляции для единичного элемента 11=10 смЗ в однородном поле следует описывать двух-параметрическим распределением Вейбулла f (£пр)=1-ехрГ-С-ПУ" (5.40) с параметрами £ар бз и 6. Необходимо найти функцию поведения электрической прочности кабеля с произвольными внутренним и внешним радиусами {гг; п) и длиной /. В качестве предварительных допущений примем, что все распределенные по объему кабеля частицы могут вызвать пробой под действием одного и того же зависящего от напряженности поля механизма и что пробой одного элемента означает непосредственно пробой всего промежутка. В промежутках с большой степенью неоднородности поля (т)>0,7) эти допущения столь же оправданы, как и при малой степени неоднородности (т]<0,4). В отдельных случаях их справедливость следует контролировать. В качестве случайной характеристики будет служить электрическая прочность, которая в данном случае должна быть идентична максимальной напряженности поля пробоя. Поскольку нагрузка меняется не в осевом, но в радиальном направлении, в соответствии с присущим цилиндрическим системам распределением напряженности для зависимости оцениваемой случайной характеристики электрической прочности в элементе объема dV из (5.39) следует Епр е = EnpTilr. (5.41) Влияние на пробой увеличения объема изоляции уменьшается так же, как и влияние изменения радиуса. Соответственно получаем следующую зависимость элемента объема от радиуса (цилиндрический слой толщиной dr, см. рис. 5.1, б) dV = 2яШг. (5.42) В соответствии со сделанным допущением пробой одного элемента dV приводит к пробою кабеля. С помощью формул (5.40)-(5.42) уравнение (5.38) приобретает вид Fn (Епр) = 1 - ехр Т / £прГ1 L \ £пр бз*" 2пШг и окончательно (6=52) Fn (Fnp) = 1 - ехр / £пр Y Lv п у - \Епр,з) (2-6) Уг (5.43) (5.44) Для масштабного коэффициента в данном случае справедливо выраже- 11(2-6) (5.45) Как и при увеличении длины кабеля (см. рнс. 5.13), при описании напряженности для коаксиальной цилиндрической изоляции сохраняется двух- Рис. 5.24, а. Влияние на пробой изменения объема изоляции при радиальном увеличении коаксиального цилиндрического Промежутка длиной 1 м (пример 5.5) при R/r=l,b а) 1,0 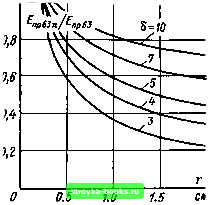 ЧрбЗп/ прбЗ SJ 1,0 0,8 0,6 0,4 Рис. 5.24, б. Влияние на пробой изменения объема изоляции при радиальном увеличении коаксиального цилиндрического промежутка длиной Q2 1 м (пример 5.5) при R/r=3 Электрическая прочность единичного элемента объемом 10 см в однородном поле обладает рас- „ пределеиием Вейбулла U параметрическое распределение Вейбулла и меняется лишь 63%-ный квантиль и и из уравнения (5.45) в соответствии с (5.16). Таким образом, 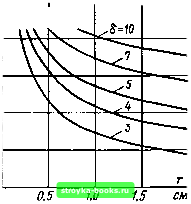 Епр йзп - •Ёпр ез Vi(2-6) 2я;г (5.46) Необходимо отметить, что столь простой учет влияния на пробой увеличения объема изоляции возможен только при сделанных допущениях (цилиндрическое поле, распределение Вейбулла). В поле иной конфигурации и при использовании другого типа распределения, как, например, при учете влияния на пробой изоляции площади поверхности, тип распределения теряется (5.34). В общем случае также и при учете влияния на пробой изменения объема следует исходя из уравнений (5.38) и (5.39) использовать численные методы решения. Если параметры распределения Вейбулла (£пр ез, 6) известны для единичного элемента объема Fi, то при сделанных допущениях относительно механизма пробоя, описываемого распределением Вейбулла, параметры (£пр 63 п, 6) могут быть вычислены в нужном диапазоне для любого цилиндрического кабеля (рис. 5.24). Кроме того, уравнение (5.46) может быть использовано также н для сопоставления различных коаксиальных цилиндрических промежутков, которым можно приписать одинаковый показатель экспоненты б [64, 300]. Если рассматриваются два промежутка с параметрами гл, щ, li и ггг, Г12, I2, то дли отношения 63 %-иых квантилей (идентичных максимальной напряженности поля пробоя), имеет место 63 2 \ k ) К Гц J 2-6 . -1 (5.47) Если оптимизируется не максимальная напряженность, а напряжение пробоя, то из соотношения между напряжением пробоя и электрической прочностью в коаксиальном цилиндрическом поле {Еир вз=£пр mai ез) следует Unp - Епр esfi In (5.48) а из формулы (5.47) для отношения пробивных напряжений пр 63 1 р 63 2 Г22 12 Г12 \(2/в)-1 -11/6 (5.49) Рисунок 5.25 показывает применение уравнения (5.49) в частном случае при 6=5, li = l2=l, Г21=Г22=Г2 кяк функции соотношеиия внутренних радиусов гц/гц. в этих условиях изменению Г11/Г12 естественно соответствует изменение длины изолирующего промежутка d = Г2 - Гц = Га - Г12 (5.50) По распределению максимумов на рис. 5.25 следует сделать вывод, что прн заданном Г12 существует некоторое оптимальное значение rnirn, т. е. оптимальная длина промежутка, которая зависит не только от изменения напряженности поля [см. формулу (5.48)], но и весьма существенно от статистического влияния объема на пробивное напряжение (подробнее см. в работе [300]). При математических выкладках следует учитывать, что влияние на пробой изменения объема Рис. 5.25. Оптимизация напряжения пробоя в коаксиальном кабеле при учете влияния изменения объема при 6=5 Распределение Вейбулла; i=a=- 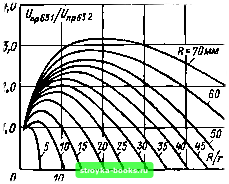 20 30 40 50 =1, Й=Л2=Л, •-1 мм, и вестно пр 63 2 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [ 93 ] [94] [95] [96] [97] [98] [99] [100] [101] 0.0015 |